Linear approximation of a combination of lines by a set of noisy points

Formulation of the problem

Let's consider the problem of approximation of a combination of straight lines by a set of noisy coordinates of points located on a given combination of lines (see Fig. 1 and Fig. 2). The usual formula of linear approximation will not work here, since the points are mixed and the result will be some averaged line between them (see Fig. 3).

Figure: 1 Line combination and noisy set of coordinates

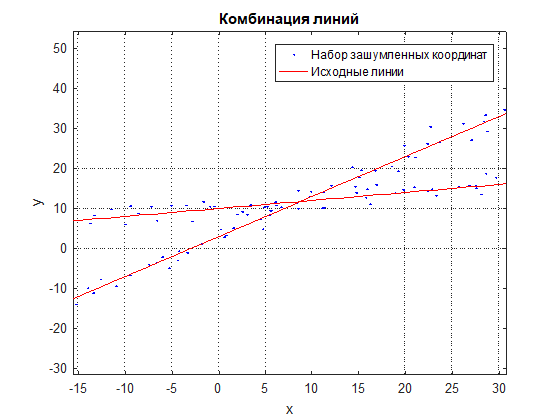
Figure: 2 A combination of lines and a noisy set of coordinates in an enlarged scale

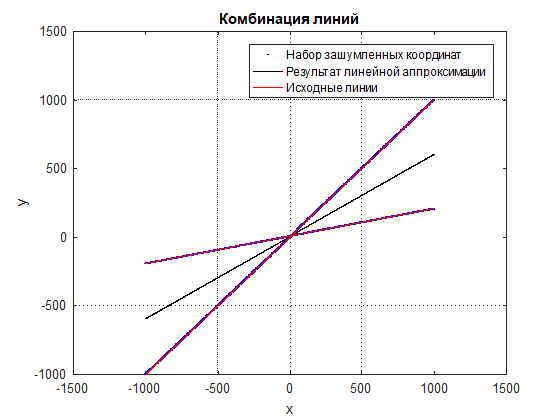
Figure: 3 Result of linear approximation

, , . .. , , -90 +90 ( -180 180 , .. ).

, , . , , . .

, , . , , .

1.

. , . , . -90 90 0.1 .

2.

, .

, , :

y = k x + b, x_{p}, y_{p}

, , , :

y - y_{p} = - (x - x_{p}) / k => y = - x / k + x_{p} / k + y_{p}

, :

- x / k + x_{p} / k + y_{p} = k x + b => - x + x_{p} + k y_{p} = k^{2} x + b k

- b k + x_{p} + k y_{p} = k^{2} x + x => x = (x_{p} + k y_{p} - b k) / (k^{2} + 1)

y = k (x_{p} + k y_{p} - b k) / (k^{2} + 1) + b = (〖 k x 〗_{p} + k^{2} y_{p} - b k^{2} + b k^{2} + b) / (k^{2} + 1) = (〖 k x 〗_{p} + k^{2} y_{p} + b) / (k^{2} + 1)

:

d i s t = \sqrt ((x_{p} - (x_{p} + k y_{p} - b k) / (k^{2} + 1))^{2} + (y_{p} - (〖 k x 〗_{p} + k^{2} y_{p} + b) / (k^{2} + 1))^{2})

3.

, , , (. . 4-6).

. , (. . 7, 8). . 7 , .

. 4 ( )

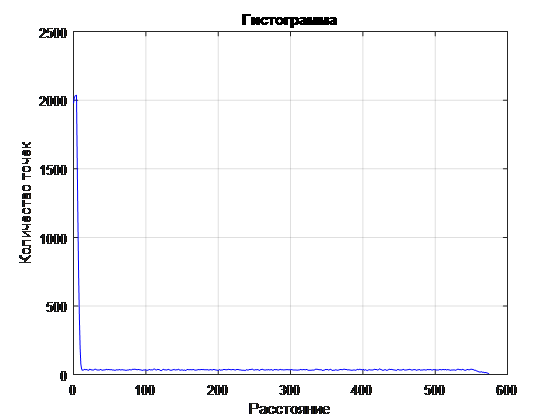
. 5 ( )

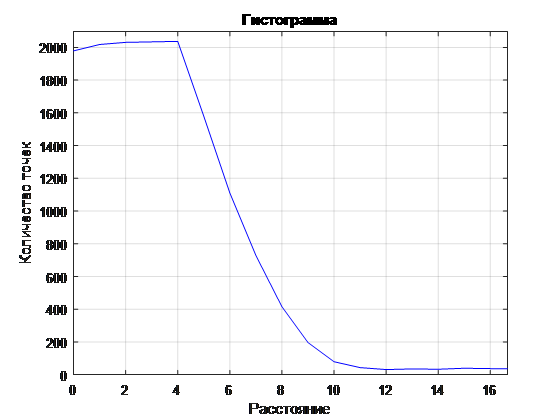
. 6 ( )

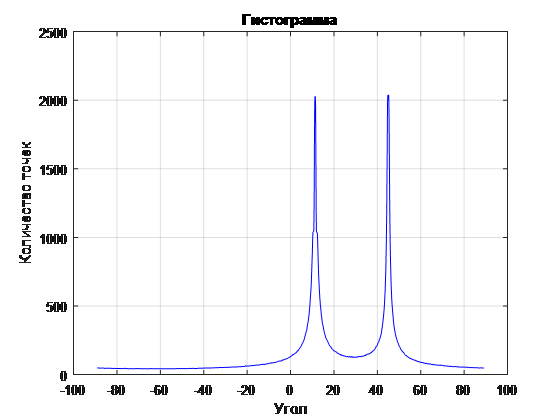
. 7 ( 1)

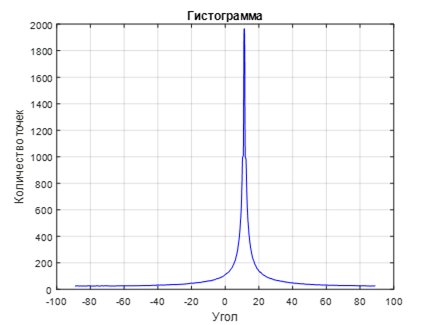
. 8 ( 2)

4.

, . , (. . 9 . 10):

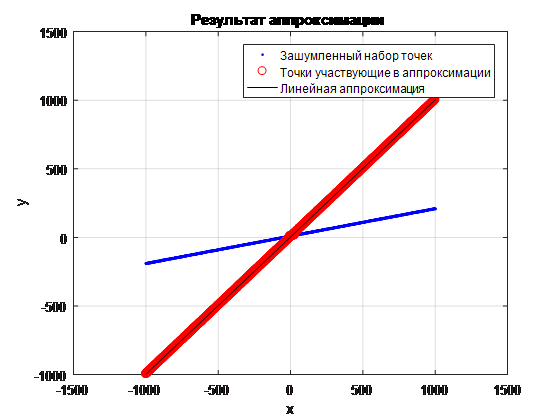
k = (N \sum_{1}^{N} (x y) - \sum_{1}^{N} x \sum_{1}^{N} y) / (N \sum_{1}^{N} x^{2} - (\sum_{1}^{N} x)^{2}); b = (\sum_{1}^{N} y - k \sum_{1}^{N} x) / N

. 9

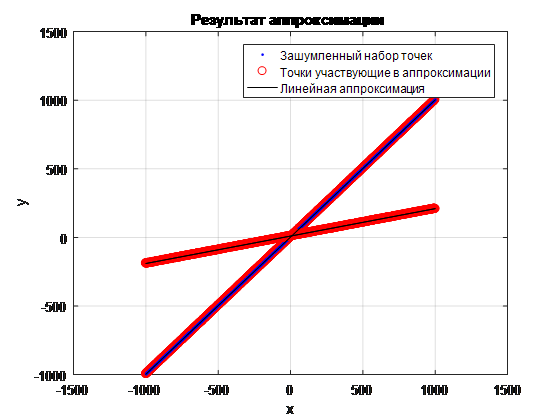
. 10

(. 11-13).

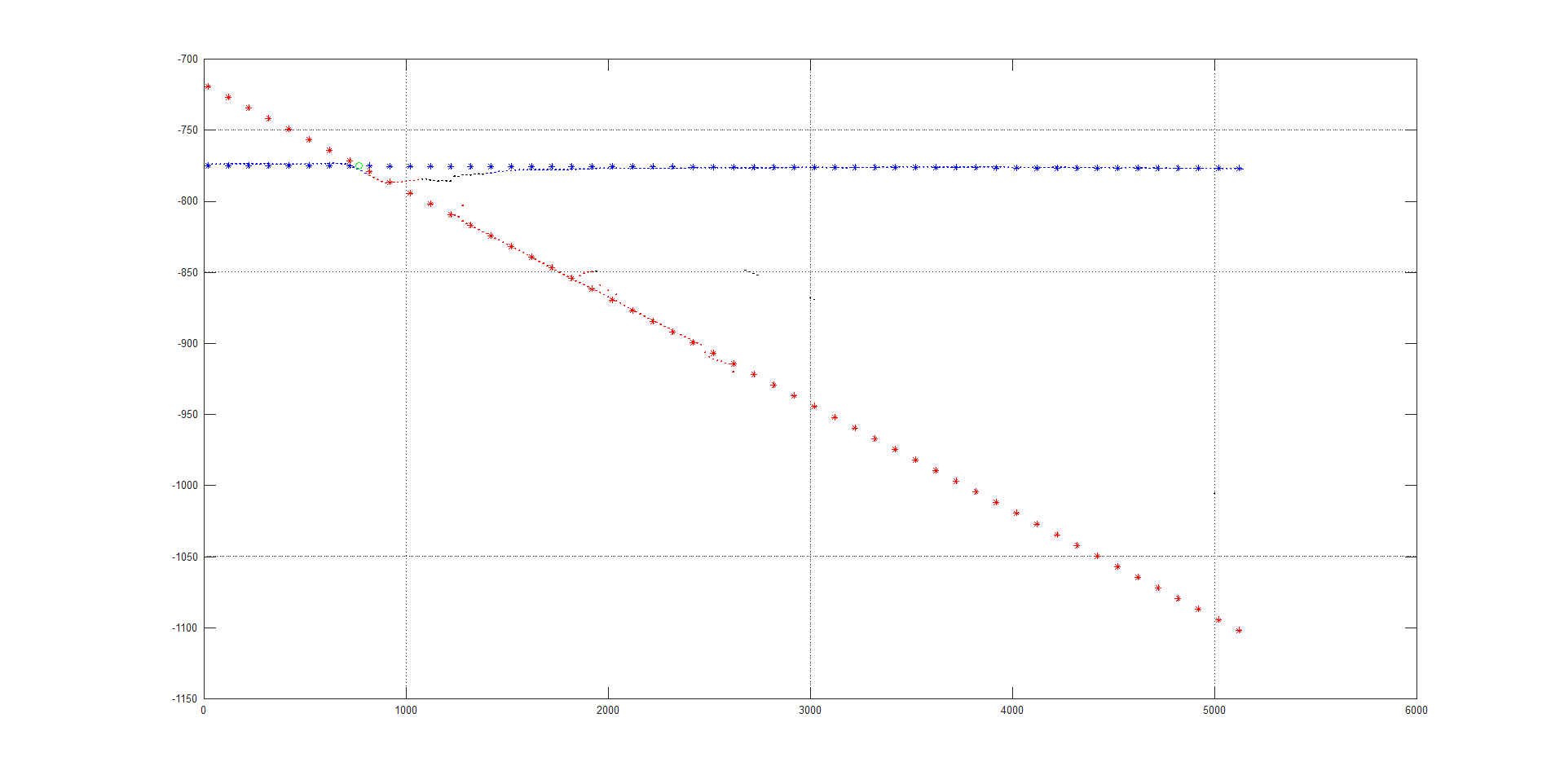
. 11

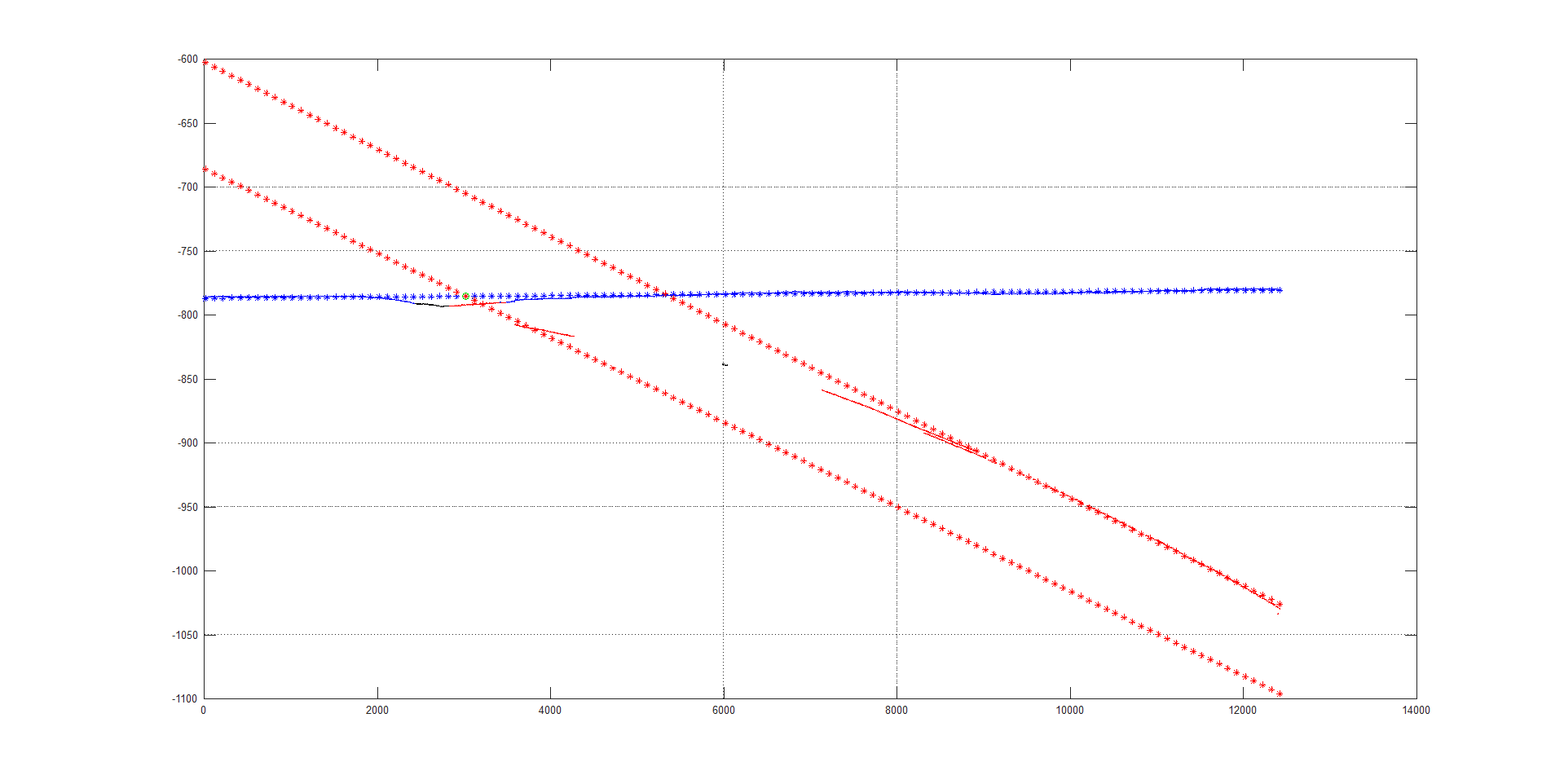
. 12

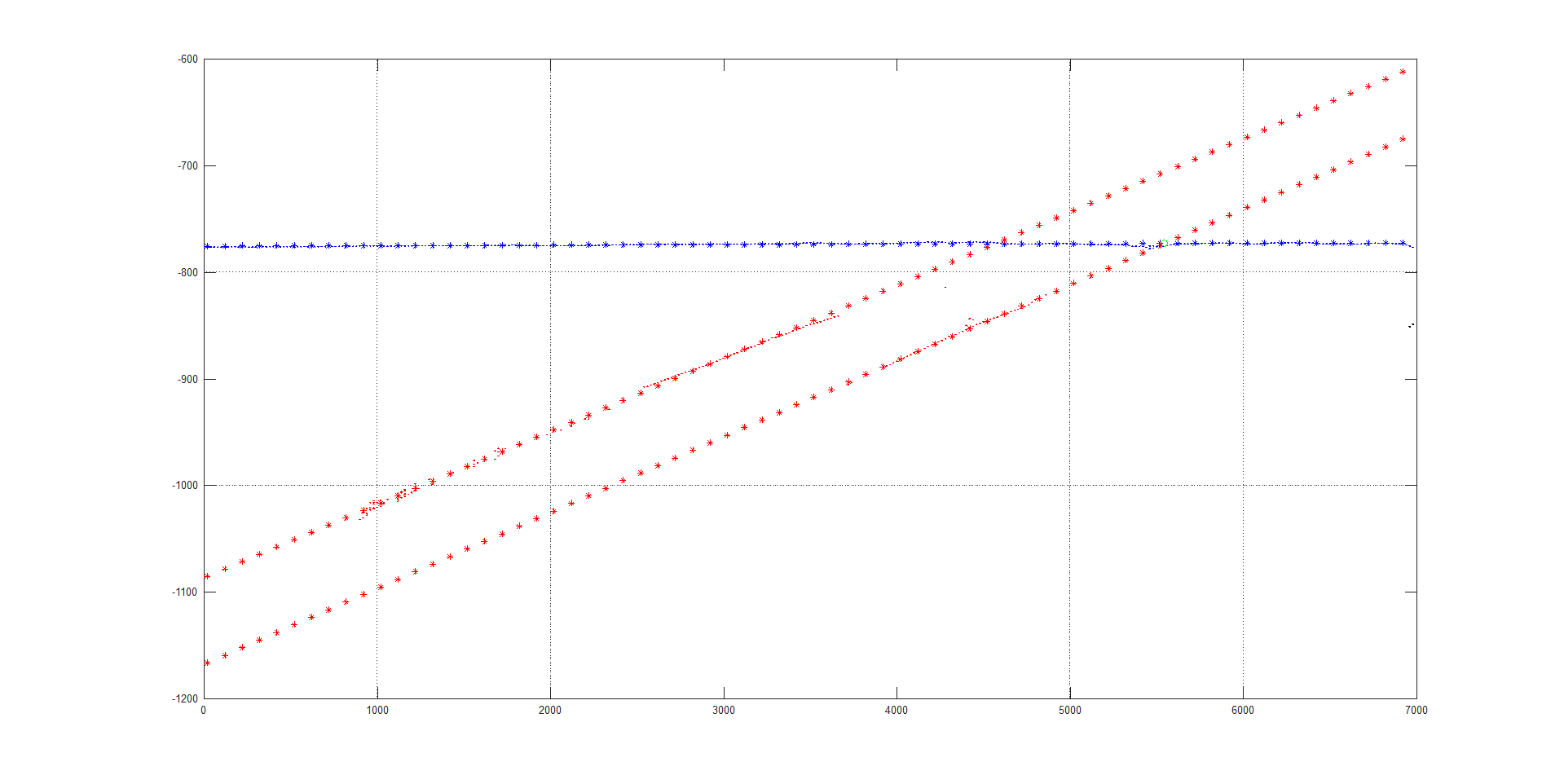
. 13

( ). .

, , , , .

, - . , . - , .

All Articles