
Other articles in the cycle
AES — . I
ES — . II
AES — . III
AES — . IV
AES — . V.
ES — . II
AES — . III
AES — . IV
AES — . V.
After a detailed presentation with details of individual transformations, with elements of a finite, not abstract (as in many publications, not excluding the Khabrovsky) algebraic field, but ( concrete ), within which RIJNDAEL, AES-128 and ( performing operations of the AES-128 standard ) are implemented , we can move on to considering possible attacks on the cipher. For now, we will confine ourselves to one attack, in our opinion, the most understandable and transparently constructed (although, perhaps, not to all readers) Habr.
I'm already accustomed to the minuses, but what the devil is not joking with. The analysis of possible attacks and expected results has been carried out by many authors, but concrete successful examples or simply impressive designs are clearly not enough. Here we will consider from a mathematical standpoint an attack using an error introduced by the intruder into the ciphertext. When choosing an attack for a demonstration, the author tried not to involve those where too twisted and abstruse mathematical things are used, but the subject in question itself is quite serious and does not allow moving on to explanations on the "fingers".
An important purpose of the publication is to show the application of mathematics, which forms the basis of AES-128, and which, unfortunately, many authors bypass or misinterpret unfounded and unsubstantiated, guided by the fact that few can check and point out their inventions.
The material of the article is not completely the original concept of the attack, the main actions are taken from the work , but it was carefully worked out, supplemented and tested experimentally by my students. They got good practice in both higher algebra and cryptology.
1. Attack on the AES cipher key
First, an attack on AES is described in a simple case, and then it becomes clear how such an attack can be generalized. The aim of the attack under consideration is to recover the key K (Nr) of the cipher. Once the partial (round) key K (Nr) is determined, it becomes easy to get the key K.
1.1 Attack principle
It is assumed that it is possible to change by introducing the error "ε" into a separate byte of the state matrix S (one of 16) after the ShiftRows (Nr - 1) operation, i.e., the penultimate round, and the index (# of the cell) of the corrupted byte (element ) state. This last hypothesis can be omitted; it was introduced in order to more easily explain the attack mechanism. The new value of the state item is assumed to be unknown.
Error "ε" extends to no more than four bytes of the exit status of the process. For all 4 changeable elements of the output state, a set of values (set) of vectors of possible error "ε" is found in section 1.4. In addition, it becomes possible to intersect the sets of possible values "ε" (definition 1) for these four elements. When such sets intersect, a smaller set is obtained, and thus the number of ciphertexts required for complete analysis is reduced.
Finally, for each error, we print out some possible garbled values for the four elements of the previous round key. Forming other ciphertexts, we find four bytes of the round key K (10). This attack remains successful even with a lot of general assumptions about the location of the error. Such as the lack of information about the location of the error before the 9th MixColumns () transformation. The difference between the cipher text matrix with and without distortions will reveal the distortions and their position (in the example, these are positions 0,7,10,13).
It is also assumed that the "ε" errors introduced in round 8 (before the 8th MixColumns () transformation) could be useful for analysis. But at the same time, the number of cipher texts required for a more complete analysis increases. For the numerical example under consideration, about ten ciphertexts are needed to obtain four bytes of the round key K (10), under conditions where the hypothesis regarding the error locations is not considered.
1.2 Numerical example of the impact of an error on a message
Here the same example is used as given in the Appendix of the named work . The penultimate and last rounds of the encryption process are considered (the byte representation of the data has the following form):
Input = '32 43 F6 A8 88 5A 30 8D 31 31 98 A2 E0 37 07 34 ';
Cipher key = '2B 7E 15 16 28 AE D2 A6 AB F7 15 88 09 CF 4F 3C';
Output = '39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32 ';
Error "ε" = '1E 00 00 00 00 00 00 00 00 00 00 00 00 00 00'.
The following diagram shows the values contained in the state arrays according to the cipher block length and cipher key length of 16 bytes each (that is, Nb = 4 and Nk = 4).
The error propagation is shown in bold and hexadecimal. Below are the squares of the State in different situations:
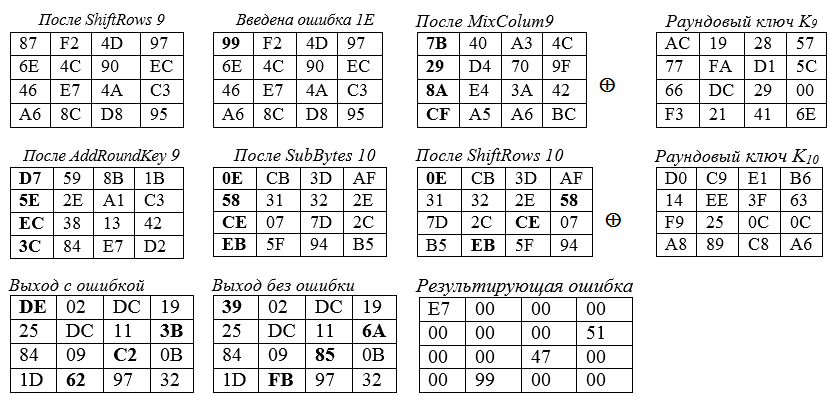
The error "ε" = 1E, inserted in the 0th byte of the 9th round status, results in changes in the four bytes of the final state. Examples of calculations for the corner cells of the main diagonal of the "square" of the state:
- the error "ε" = 1E
87 ⊕ 1E = 1000 0111⊕ 0001 1110 = 1001 1001 = 99
is entered into the upper left (corner) cell of the State square of the 9th round - lower right the 9th round State angle after MixColum9 is summed up with the key byte K (9):
BC ⊕ 6E = 1011 1100 11 0110 1110 = 1101 0010 = d2.
- calculating the values of the resulting error.
If there are two message texts with and without error, the values and positions of the corrupted status bytes are determined by subtracting one text from the other. In our case, such a subtraction can be replaced by summing the texts modulo two. We get a nonzero result only for bytes changed by an error introduced into the source text.
For example, in hexadecimal form, we find the error values:
Table 7 - calculation of error values

As a result, the difference errors... Let's give an example of calculating the last error byte:
62 ⊕ FB = 01100010 ⊕11111011 = 1001 1001 = 99.
Positions of the status bytes changed by the error
. indicate the indices for the elements of the round key (last round), as K [0], K [7], K [10], K [13]. Here, 0, 7, 10, 13 are the cell numbers of the state matrix, and the matrix Ao is the transformation matrix for mixing the columns of the encryption process, the first column of which has the form: '02', '01', '01', '03'.
How an Injected Error Affects the End Final State

Analysis of information obtained when an error is introduced
The only operation that can contain information about the key K (Nr) is the last SubBytes () transformation. Therefore, we have four equations, where x0, x1, x2, x3, ε are unknown variables.
We want to get solutions to the following four equations:
Bytes modified by an error contain information about the unknown key that generated these bytes.
All such equations can be generalized in a single equation
s (x + cε) + s (x) = ε ', (1)
where the constant value =' 01 ',' 02 'or' 03 'and it is this equation that we will further solve and analyze.
Definition 1 . The set of solutions of equation (1) for errors ε is denoted by the symbol B (cε ') and defined by the expression:
B (cε') = S (cε ') = {ε є GF [2 8 ]: ∃ x є GF [2 8 ], s (x + cε) + s (x) = ε '}, | B (cε') | = 127.
This is an individual error area corresponding to a specific error ε '. For other ε ', the error regions will be different.
Definition 2 . Consider a linear transformation ℓ over the field GF (2):
ℓ: GF [2 8 ] → GF [2 8 ];
x → x 2 + x.
The image of ℓ is a mapping of Im (ℓ) GF (2) -vector space, that is, the set of elements
(x 2 + x) from GF [2 8 ] we denote 1 = Im (ℓ) and its dimension dimGF (2) (E1) = 7. If θ є 1, then there are two different solutions x1, x2 є GF [ 2 8 ] equations x 2 + x = θ, and solutions satisfy the relation x2 = x1 + 1 and x2 ∙ x1 = θ (modd φx, (2 8 -1)) by Vieta's theorem.
The variable θ is a free term of a quadratic equation.
Let us illustrate the considered linear transformation with an example.
Example The GF field is set [2 8], the transformation x → x 2 + x is performed over its elements .
Table 8 - the initial fragment of the field GF [2 8 ] and the results of the transformation of elements.
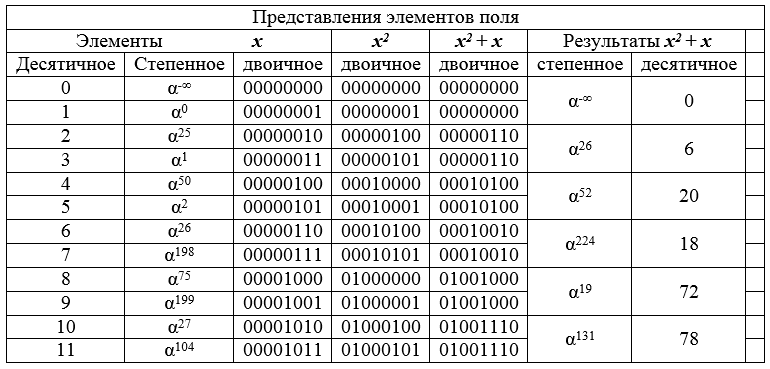
Table 8 shows how the conversion changes adjacent pairs in a decimal-ordered list to the same field element. It follows from this that the result of the transformation (image) is two times less than the preimage (the field is, as it were, compressed by 2 times). This principle of contraction of the dimension of sets forms the basis of the proposed attack.

Proposition 2 . The following statement is true for λ1, λ2 є GF [2 8 ] - {0}:





2. Generalization and implementation
First of all, using a special software application, 20 ciphertexts with an error are generated. For this, the source text, the key, the error are entered into the model (program) and the position number in which the error is placed is set. By pressing the "Start" button, the program implements the algorithm and displays the results of the last 2 rounds of encryption in expanded form for text with an error, text without an error, and the difference between them. After that, the ciphertext is saved without error and with an error. The error value is cyclically changed and by pressing the "Start" button the next ciphertext with an error is obtained. 5 ciphertexts with an error were formed on one value of the column.
To carry out an attack, it is necessary to open a file with ciphertext without error and ciphertext with an error using the program (the data in the file is presented in hexadecimal form), the ciphertexts and the difference between them are displayed as a square array of bytes (State). Pressing the button “Search for key” starts the procedure of searching for possible bytes of the key. The current state of the processes is displayed in a text box. After that, a ciphertext with another error is opened, and the procedure is repeated. When a round 10 key byte is received, it is also displayed in the corresponding square byte array. When running all 20 ciphertexts generated at the previous stage with an error, there is a high probability of obtaining the values of all bytes of the round 10 key (otherwise, ciphertexts with errors are also needed).After that, restore the encryption key according to the algorithm "Cipher key recovery using the last subkey" givenhere .
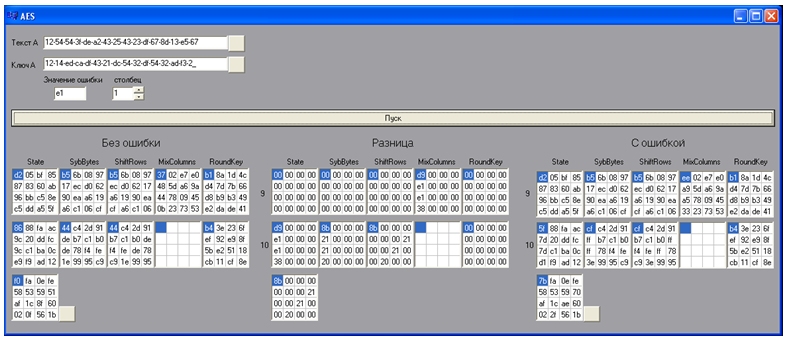
Figure 11 - Software product for constructing a ciphertext with an error
To speed up the procedure for enumerating ciphertexts with an error, you can put a tick in front of the "Find key" button
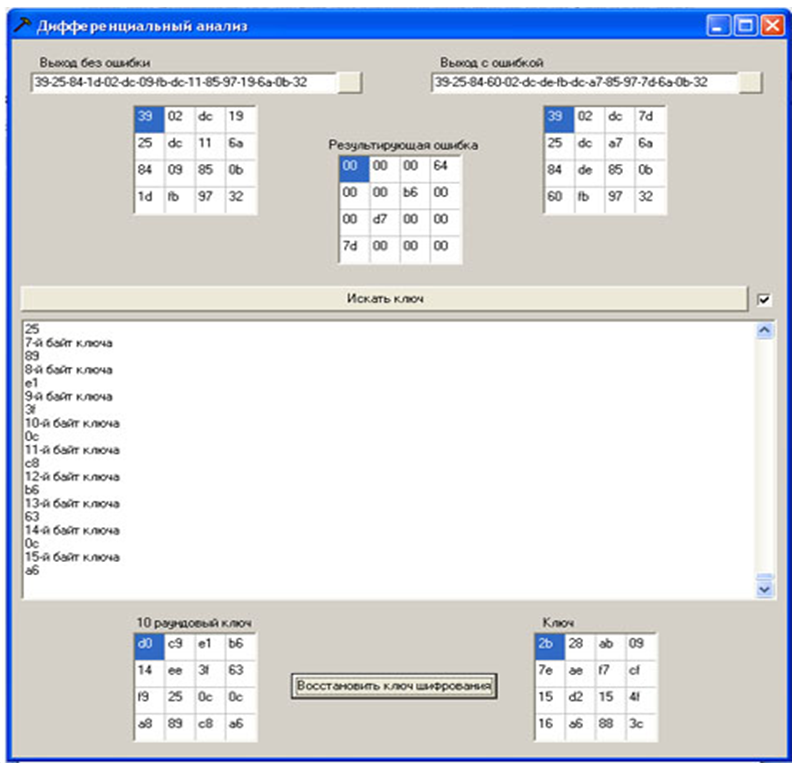
Figure 12 - Software implementation of the attack
An example of the software product operation:
Source text 3243f6a8885a308d313198a2e0370734
Key 2b7e151628aed2a6abf7158809cf4f3c
Error 1 1e000000000000000000000000000000
Ciphertext with error 1
Possible bytes de25841d02bc0962


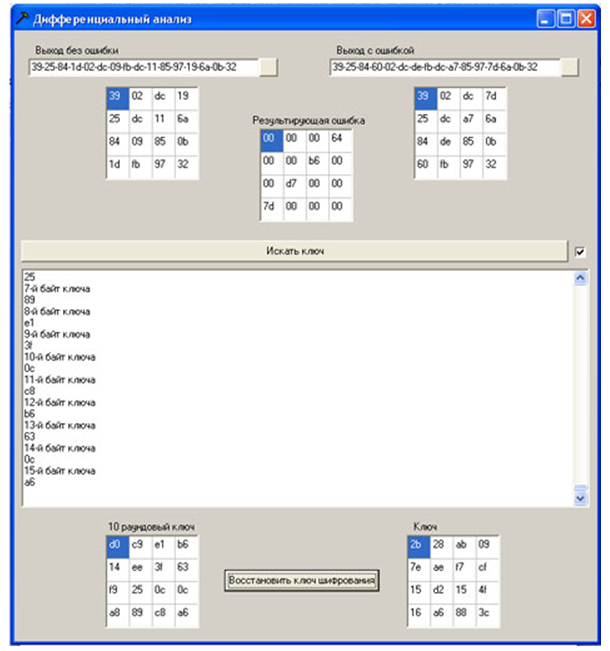
Figure 13 - An example of the program's operation
Round 10 key d014f9a8c9ee2589e13f0cc8b6630ca6 key is fully recovered
Recovered key 2b7e151628aed2a6abf7158809cf4f3c, as expected, it matches the key specified in the encryption session.
2.1. Situation when there is no error location information
At this point, it is assumed that the error is contained in the status byte between the last two executions of the MixColumns operation. This is the same case, except for the fact that the error can be enclosed between bytes from 1 to 16. The error is multiplied by the MixColumns operation and spreads to 4 bytes of status.
The forced error is generated in the first row of the differential state matrix. Here it is possible to determine which column the error entered belongs to by looking at the forced error column. This is done by examining the four possible line positions for the entered error using the method described in the preceding description.
2.2. Hardware device
Let's assume you have the ability to physically interfere with an AES hardware device. First, let's compute ciphers for more than ten random plaintext using an AES device. Then we modify the example project by cutting out the lines and connecting them to the ground (or Vcc) temporaly between two bytes during the round, located two rounds before completion. After all, we have a byte in round Nk -2, always replaced by '00' (or 'FF').
We calculate another time the same message with the acting device. With random plaintext, a defective byte is like a random error. This single error translates into four errors in the Nk -1 round and sixteen errors in the Nk round. In this case, a deviation matrix (differential) can be obtained, with the help of which it is possible, by analyzing the error, to find the last round key.
References:
[1] FIPS PUB 197: Advanced Encryption Standard, csrc.nist.gov/publications/fips/fips197/fips-197.pdf
[2] Boneh, DeMillo, and Lipton, On the Importance of Checking Cryptographic Protocols for Faults, Lecture Notes in Computer Science, Advances in Cryptology, proceedings of EU-ROCRYPT'97, pp. 37-51, 1997.
[3] E. Biham & A. Shamir, Differential Fault Analysis of Secret Key Cryptosystems, CS 0910, Proceedings of Crypto'97.
[4] Ross J. Anderson, Markus G. Kuhn: Tamper Resistance - a Cautionary Note, The Second USENIX Workshop on Electronic Commerce Proceedings, Oakland, California, November 18-21, 1996, pp 1-11, ISBN 1-880446- 83-9.