The mathematical model of the phenomenon postulates that all processes take place in 4-dimensional space-time, in which the SRT phenomena follow from the preservation of the interval of events during the transformation of the rotation of the coordinate system. It can hardly be denied that reality is, as it were, stretched over mathematical constructions. Moreover, the fact that imaginary numbers, in reality unimaginable, play an almost entirely important role in them, does not diminish the success of science. Even E. Mach said that explanations are superfluous if the observed phenomena are well described by formulas. And let's not argue with this empirio-criticism.
Mathematicians invent abstractions and try them on to reality. Hence the Singularity, wormholes and other exotic things. Or maybe it’s worth fantasizing , for example, about what would change in our ideas about the world if the cause of the Lorentz contraction were some hypothetically assumed physical mechanism. Why not?
1 the physical cause of Lorentz contraction
First, I will express the seemingly obvious maxim that particles, atoms, molecules interact with each other through physical fields . We can, of course, say that they exchange quantum particles, but we are now playing on the field of relativistic theory, so for now we will forget about quanta. So, the first fantastic assumption is that it is precisely due to the mutual balancing of field effects that the particles are added to a certain configuration and form bodies . If some particle deviates from the equilibrium position, then a field disturbance will run from it, which will move the rest of the particles, which, in turn, will cause a reverse field effect from them on this particle.
And the second assumption is thatfield disturbance propagates in a certain common space with a certain certain speed . And the fantastic nature of this assumption is that, according to science, the field exists by itself in 4-dimensional space-time (P-W) and does not spread over anything. In general, it is difficult in science ... We will assume that the fields spread and exist in a single 3-dimensional space - in which we are, the Earth and the stars. It seems that this goes without saying and who does not know, but let's see what happens. Those who are not interested in bothering with formulas can limit themselves to reading only the selected text.
So, we agree that there is an interaction time between the particles, which is made up of the time of arrival of indignation to them and the time of return of the response from them back. As a result, the previous configuration of the body will gradually be established again. Fig.1 Field influences that determine the position of the particle
For any point of the body, it is possible to distinguish groups of points with which it will have equal interaction times and which we will call isochronous with this point. The situation is reflected in Fig. 1. Naturally, at rest, the sphere of any rest radius R around a point is the locus of points (GMT) isochronous with it.
Note that the motion of a particle at each moment is determined by the sum of the resultant forces that are applied simultaneously from the totality of all groups of particles isochronous with it... Let's try to find out how the surface of the GMT, formed by a set of points 2, 3, etc., will change when the body moves. with the same interaction times with point 1, which may no longer be a sphere.
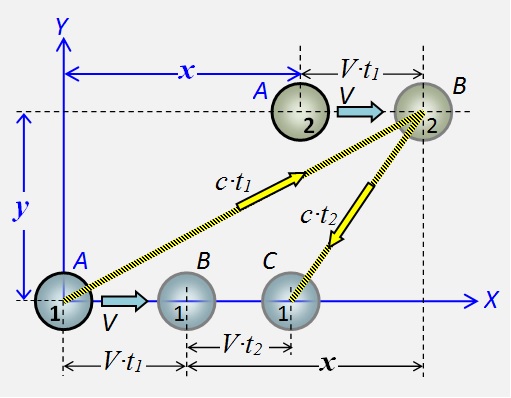Let body points 1 and 2 are fixed mutually and synchronously moving the right with velocity V . When one point is at the origin, the perturbation field is sent to the point 2. The mutual arrangement of the points marked with the letter A . Fig.2 Scheme of field interactions of points of the body - back and forth
When the disturbance reaches point 2, it will travel the distance V ∙ t 1 . Positions marked points with the letter B . During the time the disturbance returns from point 2 to point 1, point 2 will cover the distanceV ∙ t 2 . Their new position is marked with the C .
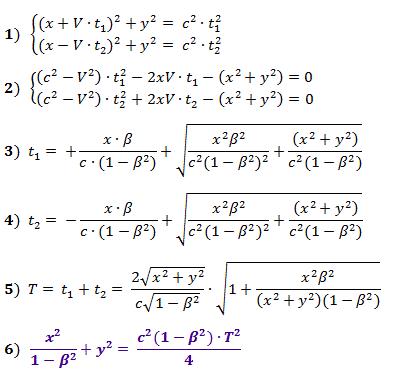Formulas (1), according to the Pythagorean theorem, describe the distances in Fig. 2, and the obtained from them (2) are equations for calculating the times t 1 and t 2 , the values of which are given by formulas (3) and (4) for positive values of the roots, where β = V / c .
Formula (5) gives the value of the interaction time from sending a disturbance to receiving a response.
From (5) we obtain equation (6) for the coordinates x and y of the geometric place of isochronous points with which the interaction time of point 1 is the same.
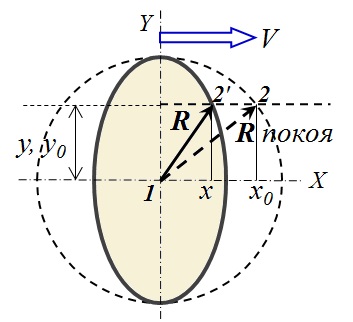Formula (6) describes the ellipsoid shown in Fig. 3, compressed along the direction of motion (along the X-axis) by √ (1 - β 2 ) times, that is, according to the Lorentz formula. Point 2 on the surface of the sphere at rest, while moving, will move to position 2 ' . In this case, material points that were isochronous with point 1 at rest will remain isochronous with it during movement . Fig.3
So, when moving, a material object is compressed according to Lorentz precisely because the very "picture" of physical fields is compressed, which ensures its integrity in space .
Since the Lorentz contraction is the same for all isochronous points surrounding each point of the object, then the entire moving object will equally proportionally contract along the axis of motion.
2. Derivation of the formula for time dilation
Let us determine the interaction time when the object is moving in comparison with the interaction time at rest.
Formulas (7) relate the coordinates of points during movement with their coordinates at rest in accordance with
equation (6). The formula (8) calculates the interaction time at rest. Formulas (9) and (10) were obtained from formula (6) by substituting into it the values of coordinates x and y and R of rest from formulas (7). Formula (11) is equivalent to (10). Formula (12), obtained from (11) by substituting the left side of formula (8) into it, connects the interaction times at rest and during motion. In the traditional form, this is reflected in formula (13), where T 0 is the time interval between events in a resting object, andT is the time interval between the same events in a moving body.
So, the interaction times of all points in a moving object increase in the same proportion according to Lorentz compared to the interaction time at rest. Accordingly, in general, all processes in a moving object actually slow down in the same respect .
The reason for the slowing down of time is easy to understand if we take into account that the field disturbance from the rear of the interacting particles will have to catch up with the front one in the direction of motion . When the speed of the body is almost equal to the speed of light, it will take a long time to catch up, and if the speed of the body is equal to the speed of light, it will never catch up. All changes in the body will stop and time in it will seem to stop.
3.Explanation of the phenomenon of the constancy of the speed of light, etc.
Let's do a thought experiment. Let a pulse of light be emitted from the last car of the train, which is received in its head car. We have to measure the time T 0 that the light will spend on the passage of a train of known length L 0 in its own system. In the proof, we will use the assumptions about the homogeneity and isotropy of space, in particular, we will assume the same measurement results for the first and second halves of the train, as well as for the forward and backward directions. But, strictly speaking, these assumptions are valid only within the location and time of the experiment.
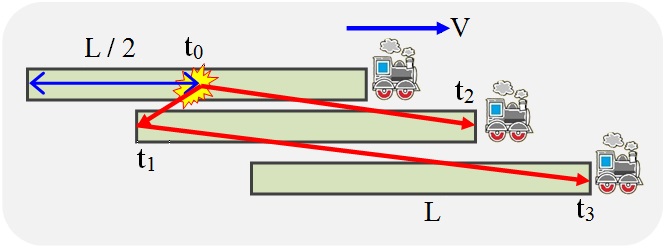
Fig. 4. Thought experiment to determine the speed of light in a moving train
To synchronize the moment of sending a signal from the last car of the train and the start of the time counter in its front car, we use a starting pulse of light from the middle of the train to both ends.
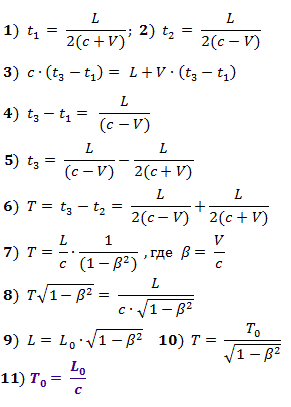
When the starting signal from the middle of the train reaches its tail (time t 1 ), a light pulse will be sent. When the start signal reaches the head of the train (time t 2 ), the countdown will begin until the arrival of the sent pulse.
When light travels to the tail, its speed is added to the speed of the train, when to the head, the speed of the train is subtracted. We obtain the relations given below in formulas (1) - (6).
Time T = t 3 - t 2 is the time interval, which,according to the observer on the train , it separates the events of the moment of sending the signal from the end of the train (from the moment of receiving the starting signal there) and the moment of its receipt in the head of the train.
From (6) we obtain formula (7), which we transform to the form (8). Further, we will take into account that all the quantities L , T and t here are measured in the reference frame of an outside observer in the space where the thought experiment is taking place. But when an object moves in space, its length, as proved in Chapter 1 , actually undergoes Lorentz contraction, and the times of events, as proved in Chapter 2, actually slow down by the same number of times, i.e. proceed longer than at rest, which is reflected in formulas (9) and (10). Substituting these ratios into formula (8) for the interval T - the travel time of light from the tail to the head of the train, we obtain relation (11).
But what relation do these T 0 and L 0 at rest have to their own time and length for the same events, measured in the inertial frame of reference (IRF) associated with a moving train? Obviously they are their equal . The fact is that time and length are numerically expressed through their relation to standards. Accordingly, measurements of the temporal and spatial coordinates of something made at rest will be numericallyare equal to the measurements of the same, made in a moving ISO, since when moving the values of both measurements and standards will change proportionally.
The question is how exactly they change when moving in space. A thought experiment with a train proves that they change in such a way that the numerical value of the speed of light measured in IFR remains equal to the value of its speed in space . This is precisely what was not a priori obvious and required proof.
We see that the "postulate of the constancy of the speed of light" is derived from the fact of Lorentz contraction alone, which is mathematically derived from the dependence of the location of material matter on the speed of propagation and configuration of physical fields in space .
To complete the picture, we also define the speed of light across the movement of the train, for example, between the walls of the carriage at a distance S 0 from each other. To do this, we measure the time of movement of the light pulse ( 2 · t 0 ) back and forth. In view of the obvious symmetry of "there" and "back" we will consider only "there". In the system of an outside observer, movement in space occurs as shown in Fig. 5.
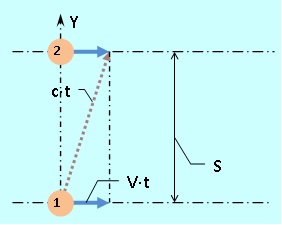Hence we have (c · t) 2 = S 2 + (V · t) 2 , whence we obtain t = S / (c · √ (1 - β²)) , where β = V / c .
In the train system, the elapsed proper time t 0connected with the time passed in space by the relation t = t 0 / (√ (1 - β²)) . Substituting this expression into the formula for t in space, we get t 0 = S / c .
Fig. 5. Thought experiment to determine the speed of light in a moving train /
In the train's own system for the same t 0, we have the relation t 0 = S 0 / c 0 . But since the transverse dimensions do not change during movement, i.e. S = S 0 , we get that c 0 = c .
I suppose there is no need to prove the constancy of the measured speed of light for an arbitrary orientation of the beam, which would only add unnecessary complexity. Considering the proven invariance of the speed of light, it is easy to derive the Lorentz transformations (L), and without any appeal to Maxwell's equations or to the mathematically abstract Minkowski space.
4. Derivation of Lorentz transformations
The event consists in the arrival of a light pulse at point " E ",
located in unchanged coordinates x ' and y' in the reference system {X ', Y'}, moving with a speed V relative to the fixed IFR {X, Y}, sent at the moment when points O and O 'of both COs coincided. Fig. 6.
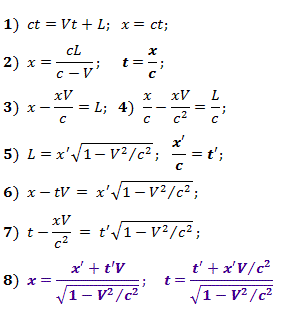In its own CO {X ', Y'} length L , measured in CO {X, Y}, the x ' coordinate will correspond . For the event, the system of equations (1) is valid, solving which we obtain (2), and then (3) and (4).
Since the lengths of bodies in motion are compressed according to Lorentz, and the speed of light, as proved in Ch. 3 , is the same in any FR, then for proper x 'andt ' in {X', Y '} relations (5) are valid. Substituting the relations from (5) into (3) we obtain (6), and substituting them into (4), we obtain (7). By virtue of the relativity of motion, we can consider the moving system {X, Y}, but then in (6) and (7) it is necessary to replace the unshaded variables with the shaded ones, and the velocity V should be taken with the opposite sign, or simply solve the system with respect to x and t .
As a result, we obtain expressions (8) for the canonical form of Lorentz transformations of coordinates and time of events in different IFRs.
When using PL as a purely formal mathematical method, the physical mechanism of SRT phenomena remains unmanifest. Therefore, in my previous articles on the relativistic Doppler effect andlight aberrations , as well as the laws of reflection from a moving inclined mirror , SLs were not used in principle to demonstrate the physical reasons for these phenomena.
5. Justification of the principle of relativity and limitations of its applicability
Note that if at rest in the diagram in Fig. 1 the disturbance from point 1 to the GMT of points isochronous with it came simultaneously, then when moving, in the diagram in Fig. 2, this is no longer fulfilled. At each point of this GMT, the response to the disturbance will be created at different times, but they will converge at point 1 simultaneously . The question is, will the result be the same as at rest?
It was proved above that in any IFR the measured proper times and distances between all points will be the same as at rest . Consequently, the number of periods, for example, initiatedelectromagnetic wave between any points will be the same as at rest. Since the perturbation of a field of an arbitrary configuration can be represented by an expansion in a series of monochromatic harmonics, the configurations and intensities of all fields in the intrinsic system will be the same at rest, respectively. Consequently, the phase relations and synchronization of the fields that form the body are not violated, and all processes in it will proceed as during rest.
This is exactly what Einstein's "principle of relativity" proclaims, and, as we see, it is mathematically inevitably deduced from two assumptions (see Chapter 1), let me remind you: first : that the position of real particles is determined by the structure of the fields , and second , thatfield propagation occurs at a finite speed .
That is, the principle of relativity is already, as it were, not a priori a universal principle , but a consequence, and has clear limits of applicability . In particular, the speed of light does not have the meaning of a world constant, but is a specific speed of light in a specific region of space . And in some places it may be different due to interaction with local physical fields, for example, gravity. So, we have two alternatives that result in exactly the same relativistic formulas:
- first, orthodox and scientific: it requires postulating a priori true principle of relativity ;
- : ,
In the first case, the phenomena of SRT do not require explanation, and their causes and mechanisms remain unknowable. The question "Why?" it even turns out to be outside of science.
In the second , the assumptions are even quite logical and nothing is required to postulate, and they are “fantastic” only insofar as other reasons for relativism are accepted in science. To the question "why are the SRT phenomena like this?" here a clear and even almost trivial explanation is given. But there is an urgent need to find out the nature of matter and in what relationship it is with physical fields.
Therefore, we will continue to fantasize further.
6. Derivation of the formula E = Mc² and the equations of dynamics
First, let us find out how the forces are transformed at relativistic velocities. Let's select the volume element in the body on which the balanced moments of forces act. When the body moves, the longitudinal size (along the trajectory of motion) of the selected element
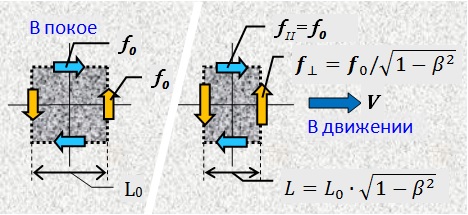will decrease in accordance with the Lorentz coefficient. For the element to remain in balance, the forces perpendicular to the movement must increase in exactly the same ratio. Fig. 7.
The magnitude of the forces parallel to the movement will not change. The factor of dependence of forces on orientation relative to the direction of motion should be taken into account in the vector expansion of forces in the following formulas.
Note that the acceleration of the body to a certain speed is carried out by the applied force, which, accordingly, does some work, thereby increasing the energy of the body. ANDWhat is the difference between a dispersed body in space and a body at rest? The fact that the overclocked is compressed according to Lorentz . In Chapter 1, a formula is derived for the locus of points (GMT) surrounding a given point, from which they have the same interaction time of physical fields. This GMT turns out to be an ellipsoid compressed according to Lorentz in the direction of motion. Let us now pay attention to the fact that the volume W of this ellipsoid decreases in proportion to the Lorentz contraction. This is reflected in formula (1) below. Now let's make a really fantastic assumption that when a body is accelerated, the work of force is spent on compressing the volume of space it occupies, which then remains unchanged in free movement. At least, this assumption is no worse than scientific maxim that space can bend or swell.
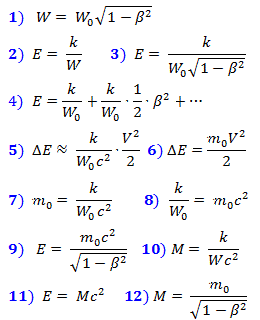Suppose that this energy E is inversely proportional to the volume to which it was possible to compress it according to formula (2), or (3) after substituting (1) into it.
We expand E from (3) into a Taylor series (4), whence (5) is the energy increment from velocity in the first approximation at low velocities. But at low speeds it is also equal to (6). Comparing (5) and (6), we obtain (7) and (8). Substituting (8) into (3), we obtain (9), which connects the energy of a body in compressed space with its rest mass.
Let us express the relativistic mass by the formula (10), whence, substituting (2), we obtain the well-known expression (11), which relates mass and energy. Comparing (9) and (11), we obtain (12).
Mass is just another formulation of the energy expended in compressing space. And in this sense they are equivalent. And the substance only "marks" the area of space occupied by the body.
Change in the total energy E of the system, i.e. the compression energy of space, in full accordance with Newtonian classical mechanics, is equal to the work of the applied force as the product of the force per path, and the change in the momentum P of the system is equal to the product of the same force and the time of its action. These dependences are reflected in formulas (13). After substituting into them the expressions for the energy from (11) and the momentum Pfrom formula (14)
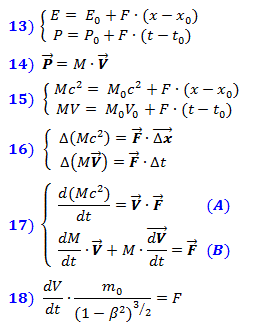we obtain the system of equations (15), which is written in the form of small increments in (16) in vector form. Then, differentiating with respect to time, we write down the system of differential equations (17) describing the relativistic dynamics. The force F does not need to be differentiated, since it is external and does not depend on the variations of the system variables. Substituting the expression for mass from (12) into formula ( A ), we obtain the well-known relativistic formula for rectilinear motion (18). 
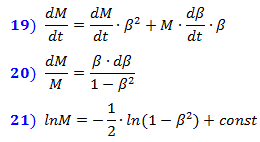From the system of equations (17) it is possible to find out the dependence of the mass on the velocity. Substituting F from formula ( B ) into formula ( A ) and dividing both sides of the equality by c², when accelerating along the trajectory of motion, we obtain expressions (19) and (20). Whence, integrating, we obtain expression (21). It is easy to see that it is equivalent to the logarithmic expression (12) for the relativistic mass, where const is equal to the logarithm of the rest mass m 0 . This means that just such a dependence of the mass on the velocity ensures the correspondence of the energy Mc² and the momentum M · V , in formulas (16, 17). And from here it also follows that the value that we previously assumed as the rest mass is a constant independent of the velocity, as it is written in the original formulas (9). And that means that our assumption about the dependence of energy on the degree of space compression is correct.
Of course, the space compression claim is not very convincing. If space is supposed to be an empty container of particles and bodies, then how can you compress the void? Emptiness will remain emptiness. Science, however, allows itself to talk about the curvature of empty space - the formulas require it. However, strictly speaking, its space is a mathematical abstraction.
But we can quite reasonably assume that space is not empty, but filled with some matter , which, suppose, not in a compressed state, is perceived by us as emptiness... When, for example, it is under compression stress, we have material particles and bodies. When these are at rest in it, the degree of compression (energy) of a section of this matter corresponds to the rest mass of the body, and with its acceleration, both the degree of compression (energy) of the body and the corresponding mass increase.
And in this material environment, physical fields that determine the location and interaction of particles (up to the "very-very" primary ones - which, we continue to fantasize , will turn out to be the phenomenon of focusing fields from their environment without which they do not exist), may well exist and propagate at a specific speed ), the rest and motion energy of which is determined by the degree of compression of the area of primary matter occupied by them . Actually,the equations of relativistic dynamics just describe the motion of these stress inhomogeneities (material bodies) in prime matter . As we could see, there are no contradictions with Michelson's experiment and Lorentz transformations.