
Source: unsplash.com
According to Jackie Stewart, three-time Formula 1 world champion, understanding the car has helped him become a better driver: "A racer doesn't have to be an engineer, but an interest in mechanics ."
Martin Thompson (creator of LMAX Disruptor ) applied this concept to programming. In a nutshell, understanding the underlying hardware will improve your skills when it comes to designing algorithms, data structures, and so on.
The Mail.ru Cloud Solutions team translated an article that delved deeper into the processor design and looked at how understanding some of the CPU concepts can help you make better decisions.
The basics
Modern processors are based on the concept of symmetric multiprocessing (SMP). A processor is designed in such a way that two or more cores share a common memory (also called main or random access memory).
In addition, to speed up memory access, the processor has several cache levels: L1, L2, and L3. The exact architecture depends on the manufacturer, CPU model, and other factors. Most often, however, L1 and L2 caches operate locally for each core, while L3 is shared across all cores.

SMP architecture
The closer the cache is to the processor core, the lower the access latency and cache size:
| Cache | Delay | CPU cycles | The size |
| L1 | ~ 1.2 ns | ~ 4 | Between 32 and 512 KB |
| L2 | ~ 3 ns | ~ 10 | Between 128 KB and 24 MB |
| L3 | ~ 12 ns | ~ 40 | Between 2 and 32 MB |
Again, the exact numbers depend on the processor model. For a rough estimate, if access to main memory takes 60 ns, access to L1 is about 50 times faster.
In the processor world, there is an important concept of link locality . When the processor accesses a specific memory location, it is very likely that:
- It will refer to the same memory location in the near future - this is the principle of time locality .
- He will refer to memory cells located nearby - this is the principle of locality by distance .
Time locality is one of the reasons for CPU caches. But how do you use distance locality? Solution - instead of copying one memory cell to the CPU caches, the cache line is copied there. A cache line is a contiguous segment of memory.
The cache line size depends on the cache level (and again on the processor model). For example, here is the size of the L1 cache line on my machine:
$ sysctl -a | grep cacheline
hw.cachelinesize: 64
Instead of copying a single variable to the L1 cache, the processor copies a contiguous 64-byte segment there. For example, instead of copying a single int64 element of a Go slice, it copies that element plus seven more int64 elements.
Specific Uses for Cache Lines in Go
Let's look at a concrete example that demonstrates the benefits of processor caches. In the following code, we add two square matrices of int64 elements:
func BenchmarkMatrixCombination(b *testing.B) {
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i++ {
for j := 0; j < matrixLength; j++ {
matrixA[i][j] = matrixA[i][j] + matrixB[i][j]
}
}
}
}
If
matrixLengthequal to 64k, it produces the following result:
BenchmarkMatrixSimpleCombination-64000 8 130724158 ns/op
Now, instead,
matrixB[i][j]we'll add matrixB[j][i]:
func BenchmarkMatrixReversedCombination(b *testing.B) {
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i++ {
for j := 0; j < matrixLength; j++ {
matrixA[i][j] = matrixA[i][j] + matrixB[j][i]
}
}
}
}
Will this affect the results?
BenchmarkMatrixCombination-64000 8 130724158 ns/op
BenchmarkMatrixReversedCombination-64000 2 573121540 ns/op
Yes, it did, and quite radically! How can this be explained?
Let's try to draw what is happening. The blue circle indicates the first matrix and the pink circle indicates the second. When we set
matrixA[i][j] = matrixA[i][j] + matrixB[j][i], the blue pointer is at position (4.0) and the pink one is at position (0.4):
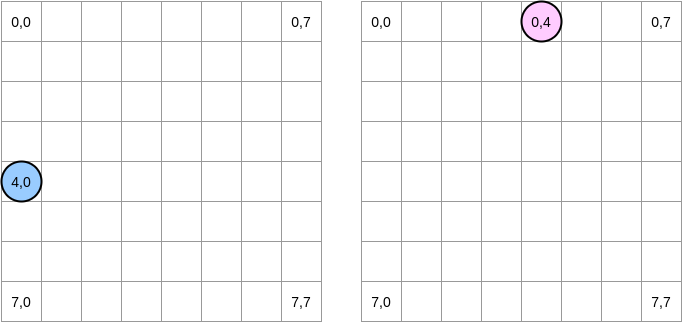
Note . In this diagram, matrices are presented in mathematical form: with an abscissa and an ordinate, and the position (0,0) is in the upper left square. In memory, all rows of the matrix are arranged sequentially. However, for the sake of clarity, let's look at the mathematical representation. Moreover, in the following examples, the matrix size is a multiple of the cache line size. Therefore, the cache line will not “catch up” on the next row. It sounds complicated, but the examples will make everything clear.
How are we going to iterate over matrices? The blue pointer moves to the right until it reaches the last column and then moves to the next row at position (5,0), and so on. Conversely, the pink pointer moves down and then moves to the next column.
When the pink pointer reaches position (0.4), the processor caches the entire line (in our example, the cache line size is four elements). So when the pink pointer reaches position (0.5), we can assume that the variable is already present in L1, right?
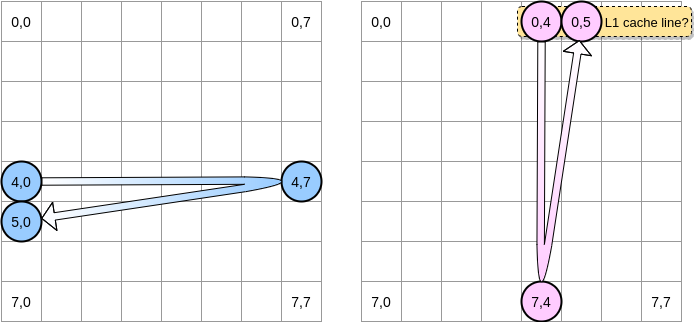
The answer depends on the size of the matrix :
- If the matrix is small enough compared to the size of L1, then yes, element (0.5) will already be cached.
- Otherwise, the cache line will be removed from L1 before the pointer reaches position (0.5). Therefore, it will generate a cache miss and the processor will have to access the variable in a different way, for example via L2. We will be in this state:
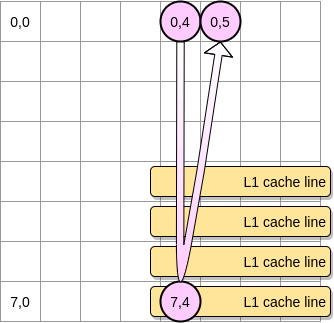
How small does a matrix need to be to benefit from L1? Let's count a little. First, you need to know the size of the L1 cache:
$ sysctl hw.l1dcachesize
hw.l1icachesize: 32768
On my machine, the L1 cache is 32,768 bytes while the L1 cache line is 64 bytes. This way, I can store up to 512 cache lines in L1. What if we run the same benchmark with a 512 element matrix?
BenchmarkMatrixCombination-512 1404 718594 ns/op
BenchmarkMatrixReversedCombination-512 1363 850141 ns/opp
Although we fixed the gap (on a 64k matrix the difference was about 4 times), we can still notice a slight difference. What could be wrong? In benchmarks, we work with two matrices. Hence, the processor must keep the cache lines of both. In an ideal world (no other applications running and so on), the L1 cache is 50% filled with data from the first matrix and 50% from the second. What if we reduced the size of the matrix by half to work with 256 elements:
BenchmarkMatrixCombination-256 5712 176415 ns/op
BenchmarkMatrixReversedCombination-256 6470 164720 ns/op
Finally, we have reached the point where the two results are (almost) equivalent.
. ? , Go. - LEA (Load Effective Address). , . LEA .
, int64 , LEA , 8 . , . , . , () .
Now - how to limit the impact of cache misses in the case of a larger matrix? There is a method, which is called the optimization of nested loops (loop nest optimization). To get the most out of the cache lines, we should only iterate within a given block.
Let's define a block in our example as a square of 4 elements. In the first matrix, we iterate from (4.0) to (4.3). Then move on to the next row. Accordingly, we iterate over the second matrix only from (0.4) to (3.4) before moving on to the next column.
When the pink pointer goes over the first column, the processor stores the corresponding cache line. Thus, going over the rest of the block means taking advantage of L1:
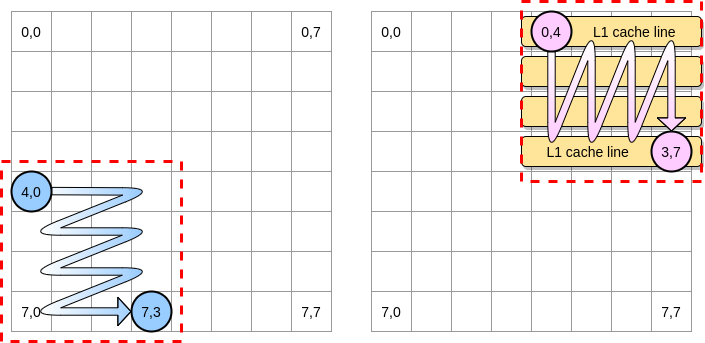
Let's write an implementation of this algorithm in Go, but first we must carefully choose the block size. In the previous example, it was equal to the cache line. It must not be smaller, otherwise we will store elements that will not be accessible.
In our Go benchmark, we store int64 elements (8 bytes each). The cache line is 64 bytes, so it can hold 8 items. Then the block size value must be at least 8:
func BenchmarkMatrixReversedCombinationPerBlock(b *testing.B){
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
blockSize := 8
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i += blockSize {
for j := 0; j < matrixLength; j += blockSize {
for ii := i; ii < i+blockSize; ii++ {
for jj := j; jj < j+blockSize; jj++ {
matrixA[ii][jj] = matrixA[ii][jj] + matrixB[jj][ii]
}
}
}
}
}
}
Our implementation is now over 67% faster than when we iterated over the entire row / column:
BenchmarkMatrixReversedCombination-64000 2 573121540 ns/op
BenchmarkMatrixReversedCombinationPerBlock-64000 6 185375690 ns/op
This was the first example to demonstrate that understanding the operation of CPU caches can help design more efficient algorithms.
False sharing
We now understand how the processor manages internal caches. As a quick summary:
- The principle of locality by distance forces the processor to take not just one memory address, but a cache line.
- The L1 cache is local to one processor core.
Now let's discuss an example with L1 cache coherency. The main memory stores two variables
var1and var2. One thread on one core accesses var1, while another thread on the other core accesses var2. Assuming both variables are continuous (or nearly continuous), we end up in a situation where it is var2present in both caches.
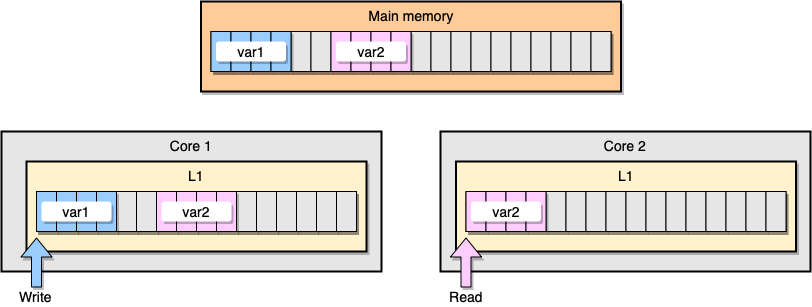
Example L1 Cache
What happens if the first thread updates its cache line? It can potentially update any location of its string, including
var2. Then, when the second thread reads var2, the value may not be consistent.
How does the processor keep the cache coherent? If two cache lines have shared addresses, the processor marks them as shared. If one thread modifies a shared line, it marks both as modified. To ensure the coherency of caches requires coordination between cores, which can significantly degrade application performance. This problem is called false sharing .
Let's consider a specific Go application. In this example, we create two structures one after the other. Therefore, these structures must be sequential in memory. Then we create two goroutines, each of them refers to its own structure (M is a constant equal to a million):
type SimpleStruct struct {
n int
}
func BenchmarkStructureFalseSharing(b *testing.B) {
structA := SimpleStruct{}
structB := SimpleStruct{}
wg := sync.WaitGroup{}
b.ResetTimer()
for i := 0; i < b.N; i++ {
wg.Add(2)
go func() {
for j := 0; j < M; j++ {
structA.n += j
}
wg.Done()
}()
go func() {
for j := 0; j < M; j++ {
structB.n += j
}
wg.Done()
}()
wg.Wait()
}
}
In this example, the variable n of the second structure is only available to the second goroutine. However, since the structures are contiguous in memory, the variable will be present on both cache lines (assuming both goroutines are scheduled on threads on separate cores, which is not necessarily the case). Here is the benchmark result:
BenchmarkStructureFalseSharing 514 2641990 ns/op
How to prevent false information sharing? One solution is complete memory (memory padding). Our goal is to ensure that there is enough space between two variables so that they belong to different cache lines.
First, let's create an alternative to the previous structure by filling the memory after declaring the variable:
type PaddedStruct struct {
n int
_ CacheLinePad
}
type CacheLinePad struct {
_ [CacheLinePadSize]byte
}
const CacheLinePadSize = 64
Then we instantiate the two structures and continue accessing those two variables in separate goroutines:
func BenchmarkStructurePadding(b *testing.B) {
structA := PaddedStruct{}
structB := SimpleStruct{}
wg := sync.WaitGroup{}
b.ResetTimer()
for i := 0; i < b.N; i++ {
wg.Add(2)
go func() {
for j := 0; j < M; j++ {
structA.n += j
}
wg.Done()
}()
go func() {
for j := 0; j < M; j++ {
structB.n += j
}
wg.Done()
}()
wg.Wait()
}
}
From a memory perspective, this example should look like the two variables are part of different cache lines:
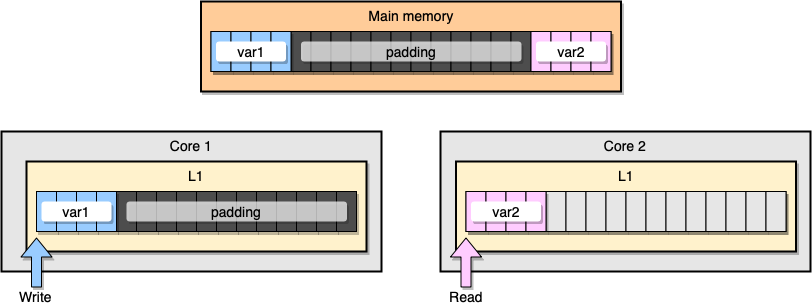
Memory filling
Let's look at the results:
BenchmarkStructureFalseSharing 514 2641990 ns/op
BenchmarkStructurePadding 735 1622886 ns/op
A second example with memory filling is about 40% faster than our original implementation. But there is also a downside. The method speeds up the code, but requires more memory.
Liking mechanics is an important concept when it comes to optimizing apps. In this article, we've seen examples of how understanding the CPU has helped us improve program speed.
What else to read:
- Three levels of autoscaling in Kubernetes and how to use them effectively .
- Kubernetes in the spirit of piracy with an implementation pattern .
- Our channel Around Kubernetes in Telegram .