- Hello everyone, my name is Rishat. I have been working on the quality of Yandex search for almost three years. But today I want to talk not about work, but about what I do in my free time. I am engaged in quantum informatics, but in fact - a variety of computation models, including quantum ones.
Quantum informatics is an interesting area right now. A lot of effort is being invested there, a lot has been done. In my report I will try to interest some of you. Maybe there is a cool ML engineer among you who wants to do quantum machine learning, or just a strong algorithmist who can invest in this direction. It will be great because the future is coming soon.
I must say right away that I am not a physicist. Surely there are people among you who understand all these processes in physics more than I do. Therefore, I will say almost nothing about physics.
I expect from you that you remember algebra a little bit, remember what a vector is and how to multiply a vector by a matrix.

How will my report be structured? First, we'll talk a little about history, about where everything came from in order to confidently look into the future. Then we'll see where this can be applied, what state is now, whether it is possible to do something with your hands right now. We will write the first Python program that can be run on a quantum computer. And then, as a bonus, I'll show you some examples of algorithms in which quantum computing helps to achieve incomparably better performance compared to classical ones.

How did it all start? From this young man. This is Alan Turing, he can be safely called the father of computer science or computer science, the one by which we all now live, make money. In the 1930s, Turing came up with a model of computation that we would now call a programmable computer. But will anyone recognize this person?

More difficult. His surname very often goes next to the surname of Turing. This is Alonzo Church, he also dealt with problems of computability, and even a little before Turing came up with his own models of computation. But Turing's work became more popular. And in general, Church at some point was Turing's scientific advisor. Taken together, their names are usually associated with this thesis.
The Church-Turing thesis says: any process can be efficiently modeled on a Turing machine. This is the late 30s - early 40s, and everything is very good. For about 30 years everything is very good, until these two people appeared. Does anyone know them?

This is already the 70s, very close to the present. Their last names are often found in cryptography courses. These are Robert Nightingale and Volker Strassen. These two people are famous for coming up with a probabilistic algorithm for checking a number for simplicity, the Solovey-Strassen test.
And this is a very important point for us, because until now we said that any algorithmic process can be modeled on a Turing machine. But now it turns out that their algorithm cannot be modeled. It is probabilistic, there is nothing like that in the Turing machine.
I had to make a quick fix and say that any process can be modeled on a probabilistic Turing machine. This is not very cool anymore, for sure one of you has a pinch in your chest. You thought: how so? Now we say "probabilistic", in ten years something else will be discovered, something else will have to be corrected. This is not very pleasant. But you and I, of course, are not alone.

There was another young man - David Deutsch. And he, too, wondered: how so? How to live? He is a physicist by training, devoted his whole life to physics. And I decided to tackle this problem from the point of view of physics. He said: let's try to substantiate, get something so that nature itself tells us that this is exactly the case. And nature already said then (and we still believe) that it is quantum mechanical. So we started looking for an answer in quantum mechanics. And it was with David Deutsch, with his first algorithms, that quantum informatics began.
This is such a small excursion into history so that you understand: it did not come out of the blue. In this area there are real problems, theoretical, of course, that torment the people who started it all.
But is everything only at the level of theory? By and large, from the point of view of mathematics, there are no problems left. Mathematically, we know everything about how a quantum computer should work. Now there are already real quantum computers of different configurations, working in different ways. And this is, by and large, an engineering challenge.
For example, at our institute we have a whole department that deals with quantum informatics. There are mathematicians and physicists. Physicists are now very closely engaged in the problem of long-term storage of quantum information. It's very similar to our hard drives, but we want quantum information to be stored there.

What are the uses of this entire economy? Of course, the first thing that comes to mind is the modeling of processes, because the world is quantum-mechanical. And if we use a quantum computer to simulate processes, chemical reactions, or whatever, it will be much cheaper computationally.
The second and very large section, to which a lot of efforts are now devoted, is quantum machine learning. There is great hope that quantum computing will help speed up the learning processes themselves and improve algorithms. There is a lot of work here. Now, for example, our quantum group is working together with a scientist from China. He is a very strong ML engineer, and we have a bit of a quantum bias, trying to come up with something together.
The third thing was a bit hype a few months ago. Now, maybe the hype is already asleep, but there is even a whole quantum blockchain. It was invented by my good friend and great friend. This is me, I say a little proudly.
But we don't have a quantum computer. Unfortunately, we cannot come home and run programs as easily as we program in Python.
What to do? I was thinking about what to do in my third year when I was writing my first term paper. I was writing a quantum computing emulator. Of course, everyone writes emulators and everyone uses them somehow. In my fourth year, I wrote an emulator that simulates interference, noises, and so on. And then I got bored.
I tried to search in a search engine and realized that there are many emulators. Here are some links, they are quite simple and interesting:
- github.com/quantumlib/Cirq
- github.com/artiste-qb-net/qubiter
- code.google.com/archive/p/pyqu
- qiskit.org
But I want to stop at qiskit. He is special, stands out from all. Than?
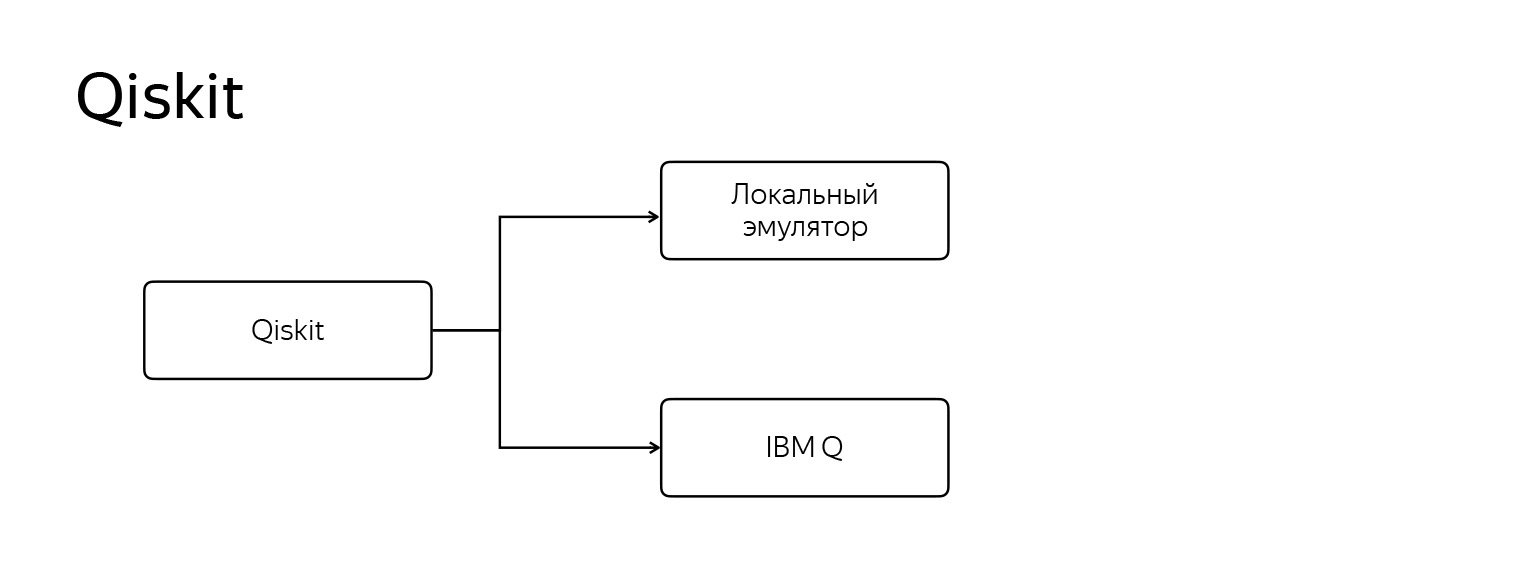
It works in two modes. The first is, like everyone else, a regular local emulator. The second is to run your program on a real IBM Q quantum computer, which looks something like this.

Now it is a whole barrel in which an extremely low temperature is maintained - about three millikelvin. It is very cold. And IBM provides the cloud-based ability to connect and run your code right on that machine.
Of course, he compiles commands and so on in a special way. How does it even work? There are several installations of such a computer for general access. One of them is 5-qubit, there is 15-qubit, 16-qubit, even 20 qubits are available to us. This is about 20 bits of ordinary, classical information, but already something.
Here, for sure, many of you think: that's it, I want it! But you have to remember a little math. A little bit of algebra, but just a little, as I promised.
To start programming on a quantum computer, you need to understand what a qubit is. It's just a vector in 2-D vector space. But since we are talking about vector spaces, they have a basis.

The basis looks something like this. There are two vector columns and a unit basis, standard, in algebra courses it is denoted as follows:
and
. And there is a standard notation in Dirac's notation, in these angle brackets.
That is, so that you do not get confused, I will continue to shorten like this.
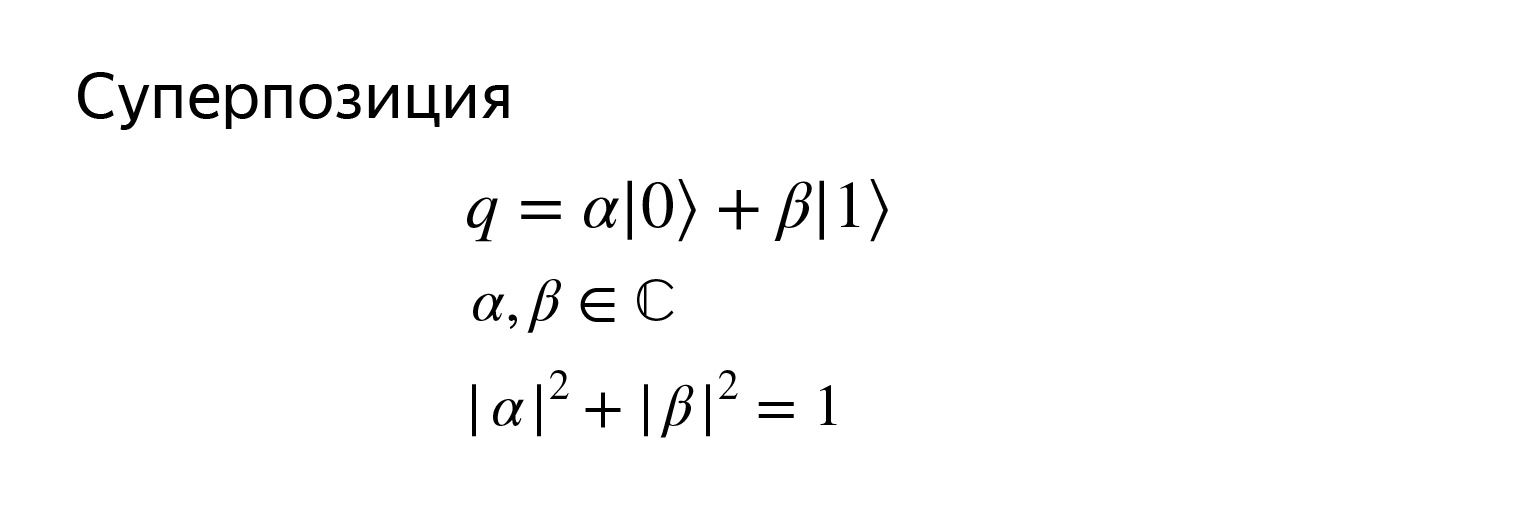
And since it is a vector, its state can be written like this. A qubit q is a superposition of two basis vectors, where α and β are complex numbers, but not absolutely any numbers, but so that the sum of the moduli of their squares is equal to one.
If we try to draw this thing, we get that a qubit is a vector on a three-dimensional sphere. An infinite amount of information can be stored in one qubit, because it is just a vector, of which there is an infinite amount.
You don't need to pay attention to the picture, it's just a visualization technique to attract attention.
We talked about qubits. Most importantly, a qubit is a vector. Vector in complex vector space. What can you do with it?
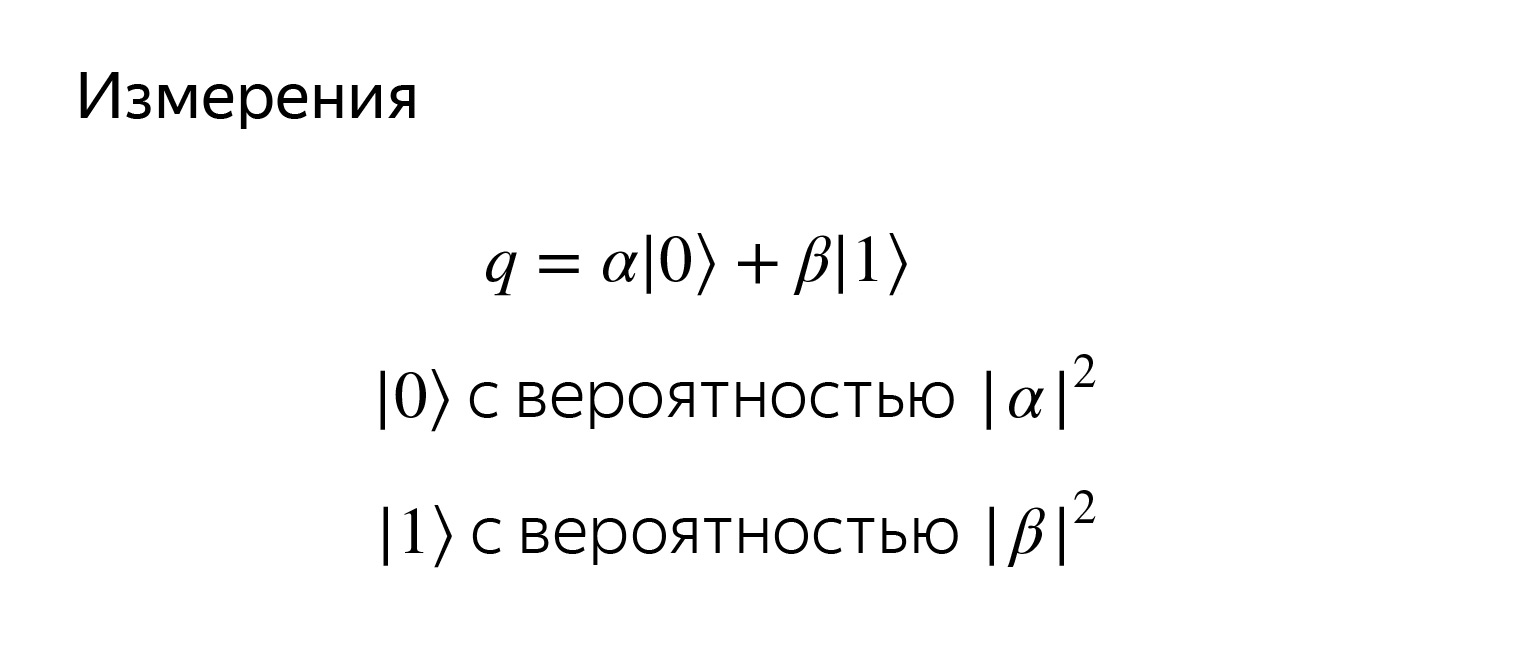
The first thing we used to do is try to calculate the value of our variable, for example, in Python. We want to read what state the qubit is in. But we will never know the exact meaning of α and β.
If we try to look at a qubit, read it, then we get either a zero or one with the corresponding probabilities. Probabilities are simply projections onto the corresponding basis vectors.
The second thing we can do is, for example, clone a qubit. We call this assigning one variable to another. Unfortunately, this cannot be done in the quantum world.

There is no assignment operation, and this is very related to what I just said: we won't even be able to look at the exact value. This is a fundamental result. It is proved very simply : literally two lines of comparisons, by contradiction.
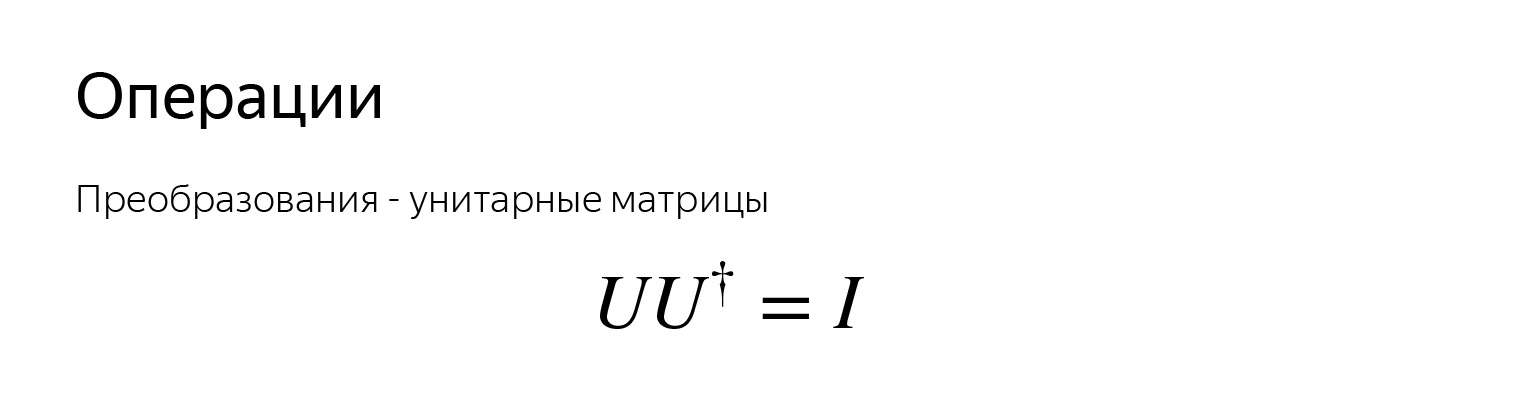
There is a qubit that we cannot read, we cannot clone. What can you do at all?
A qubit is a vector. The vector can be taken and rotated around the sphere. To rotate, you can think of a matrix that makes this rotation. All operations on qubits are matrices. They are called unitary.
Unitary - for such a condition to be met, it is written here in a cunning way. This icon denotes transposed and complex conjugate matrix. This property is very important, it means that there is an inverse for any operation. That is, no matter how we twist the vector, we can always return it to its previous position. There is always a reverse operation.
Let's see what operations can be. What we are used to in the classic case. There is a zero, you can turn it into one and vice versa.
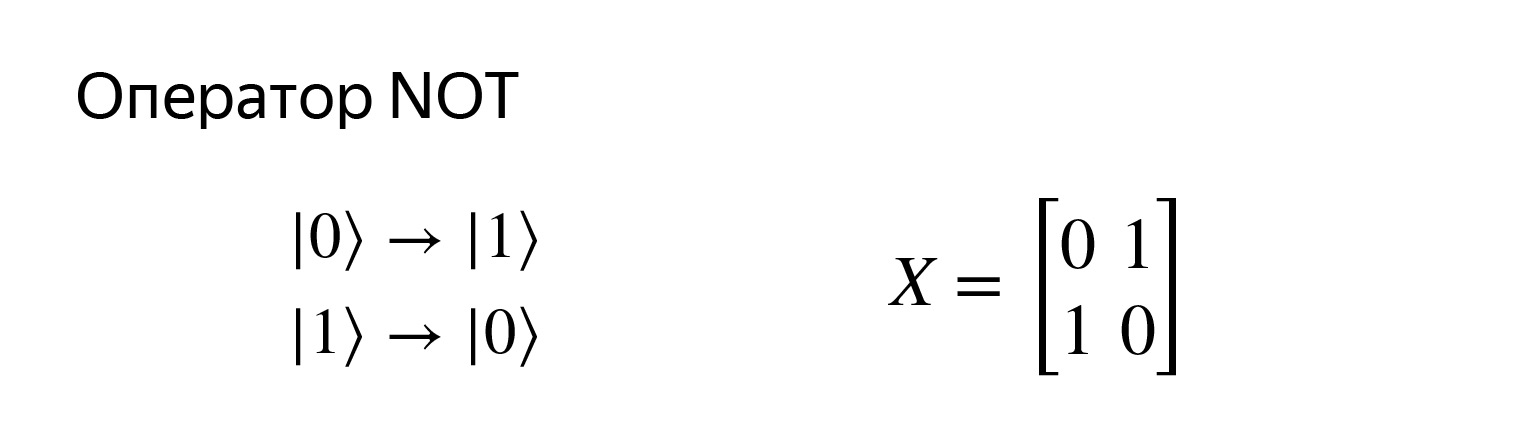
This is the negation operator and is very simple. It is recorded with such a matrix. If we try to multiply, we get exactly what we want.
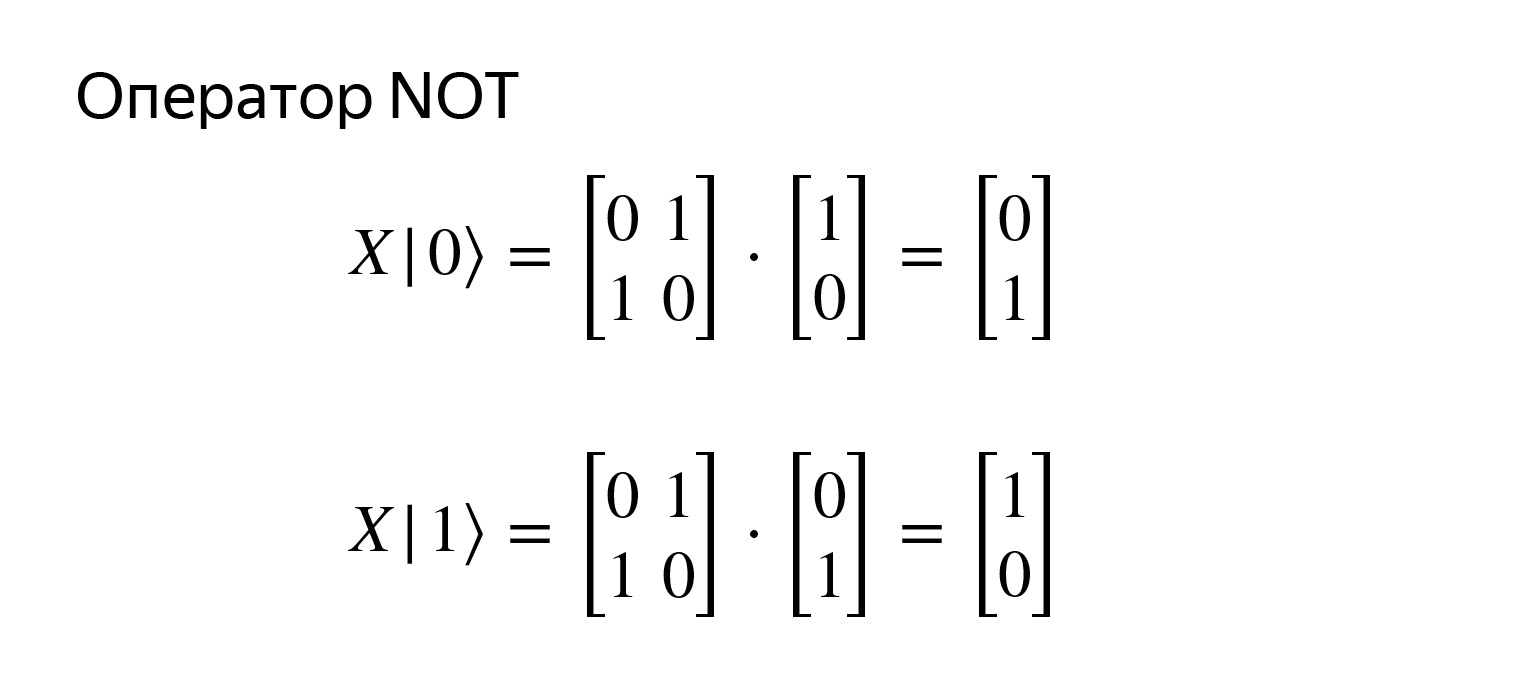
I even have it drawn here. Nothing complicated. The negation operator has a standard notation, the X operator. Come to think of it, it's just a rotation around one of the axes. And there are operators Y and Z, rotation around other axes, but this is not so important now.
And we can already run our first program on a quantum computer that will negate a qubit.
But we in quantum computer science, of course, very rarely write in Python. We use schemas more often.

The diagram usually looks like this. The horizontal lines are simply qubit values. I have five of them drawn here. And in the block - the operation that we will do.
First block. A measuring device is drawn here. This means that we just want to measure what is in the first qubit.
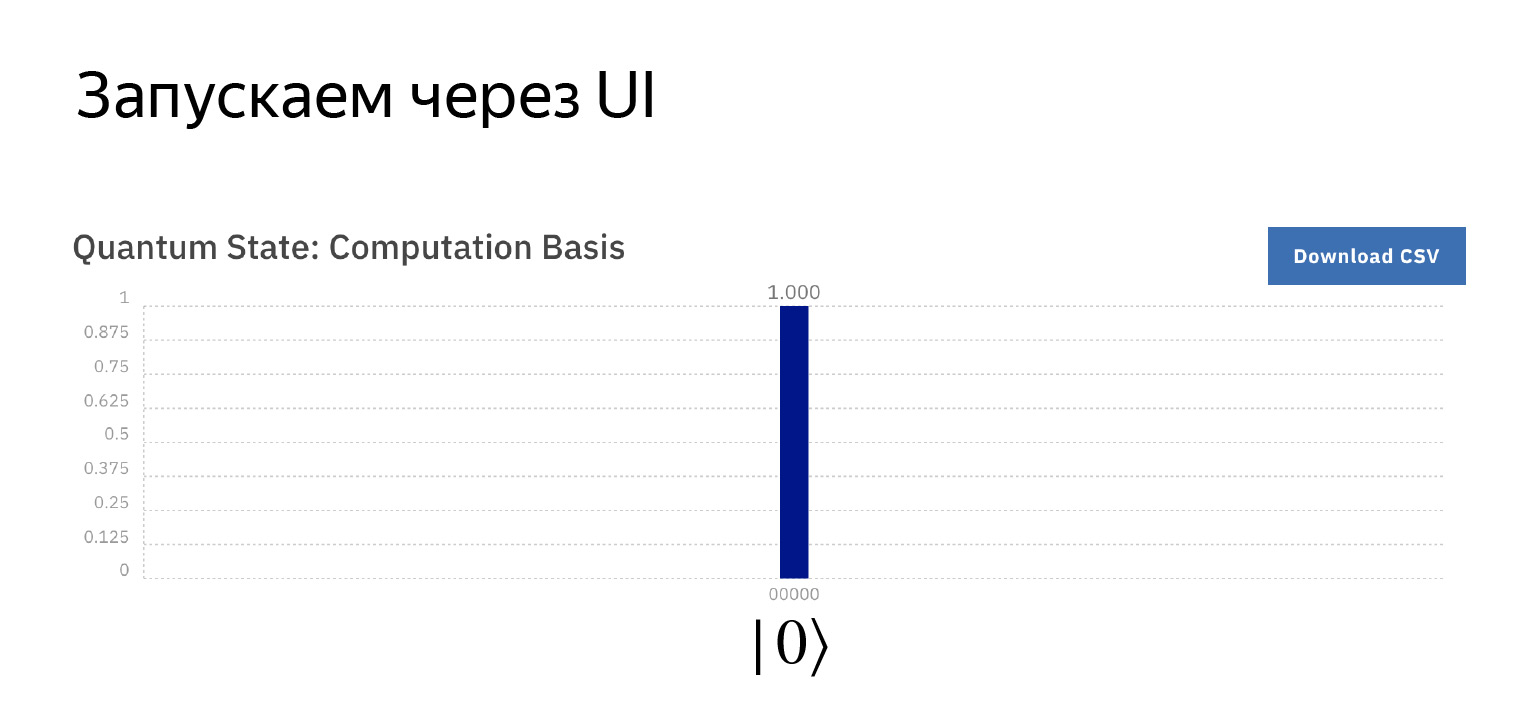
If we run this thing, we get that with a probability of one we have a zero there, because they are initialized in this state and we didn't do anything with them.
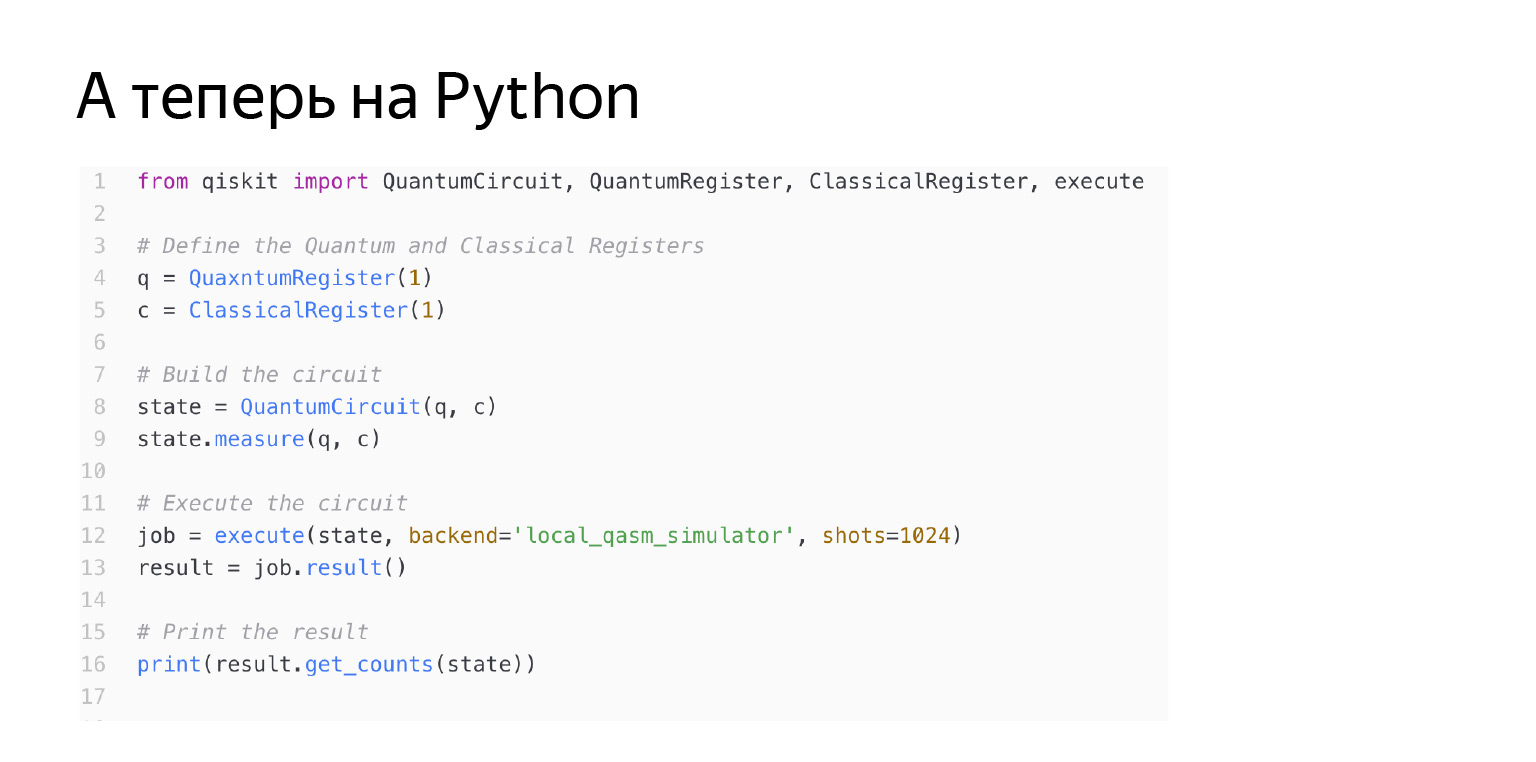
Such a thing can be written in Python using the qiskit library. Let's see what happens here line by line. First, we start the quantum register. I am turning it on here from one qubit. And the classic register. The classic register is needed to write the measurement result somewhere. That is, I do transformations with a quantum register, the result is a classic one - zero or one. And then I create my own circuit, which has this quantum classical qubit. I'm just saying: let's measure the q qubit in C. Let's start this whole thing and everything will be fine. But the attentive reader will see: it says here that my backend is a local emulator.

The same can be done with IBM Q, but there is a little more code here. There are all sorts of noodles about choosing a device that will respond to us as soon as possible, transferring some tokens, that's all. But there is nothing tricky.

The same can be done with the negation operator. This is the X operator, as I said. It looks exactly the same on the diagram, let's run the same.
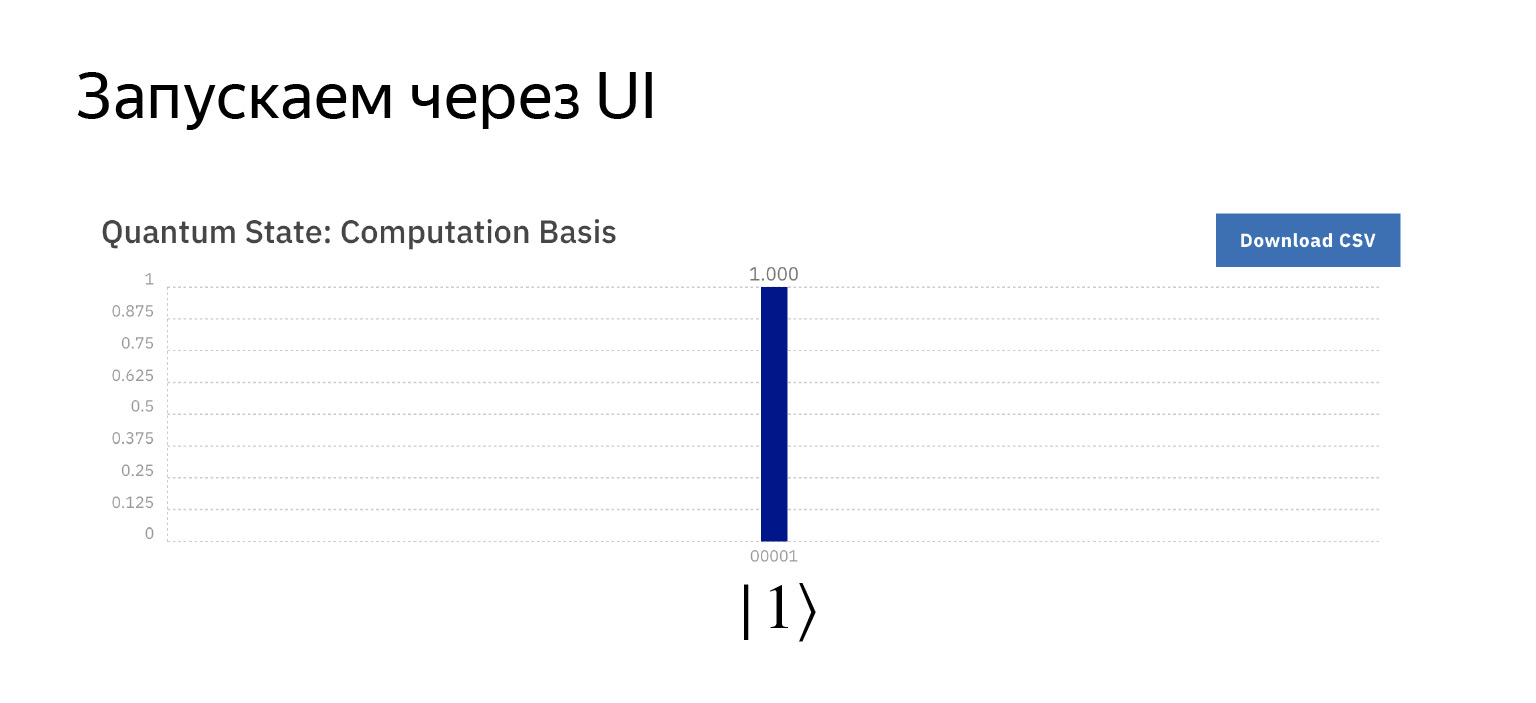
Now, with a probability of one, we get one, as planned. No magic.
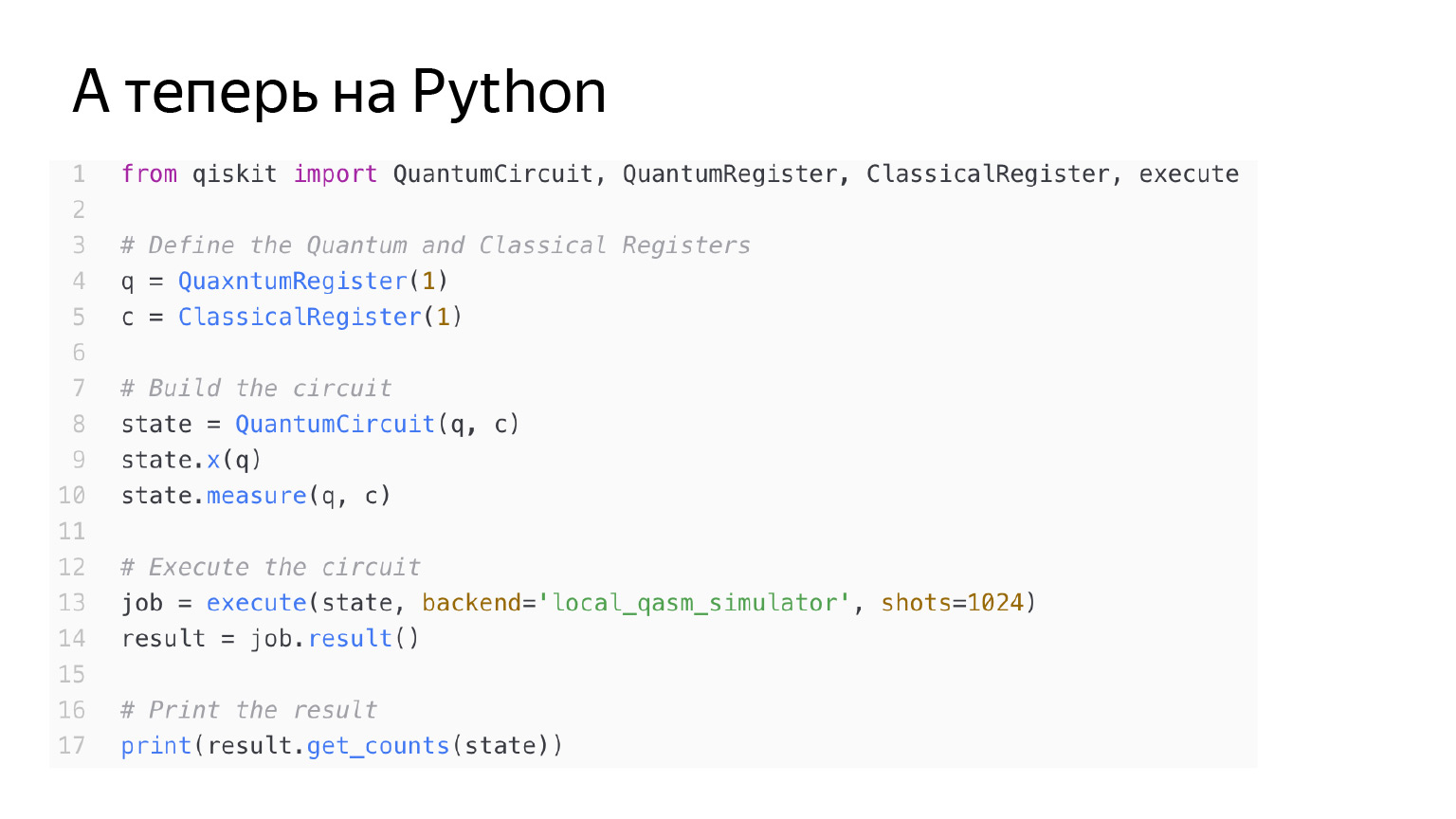
The code is the same. It's just that here I am also applying the X operator to the q qubit.
Okay, let's try to go further.
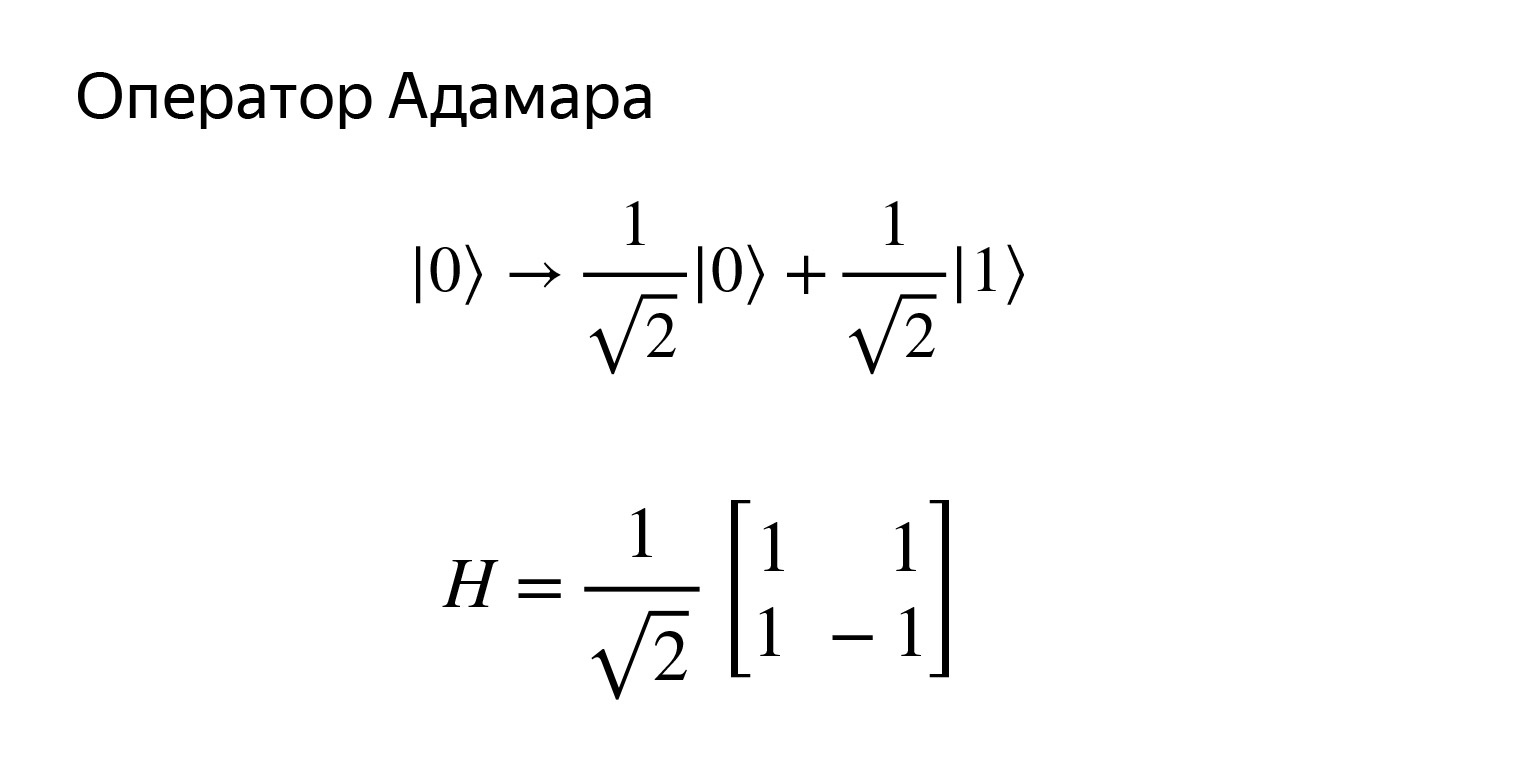
There is a very tricky thing here. Let's try to get this state. This state is very interesting. We will get such a superposition. If we try to measure it, then with a probability of 1/2 we get either zero or one. That is, it will be such a uniform superposition, we can get anything.
An analogy can be drawn to what is a quantum coin toss. We'll say okay, with probability ½ we get zero and one. The matrix looks like this.
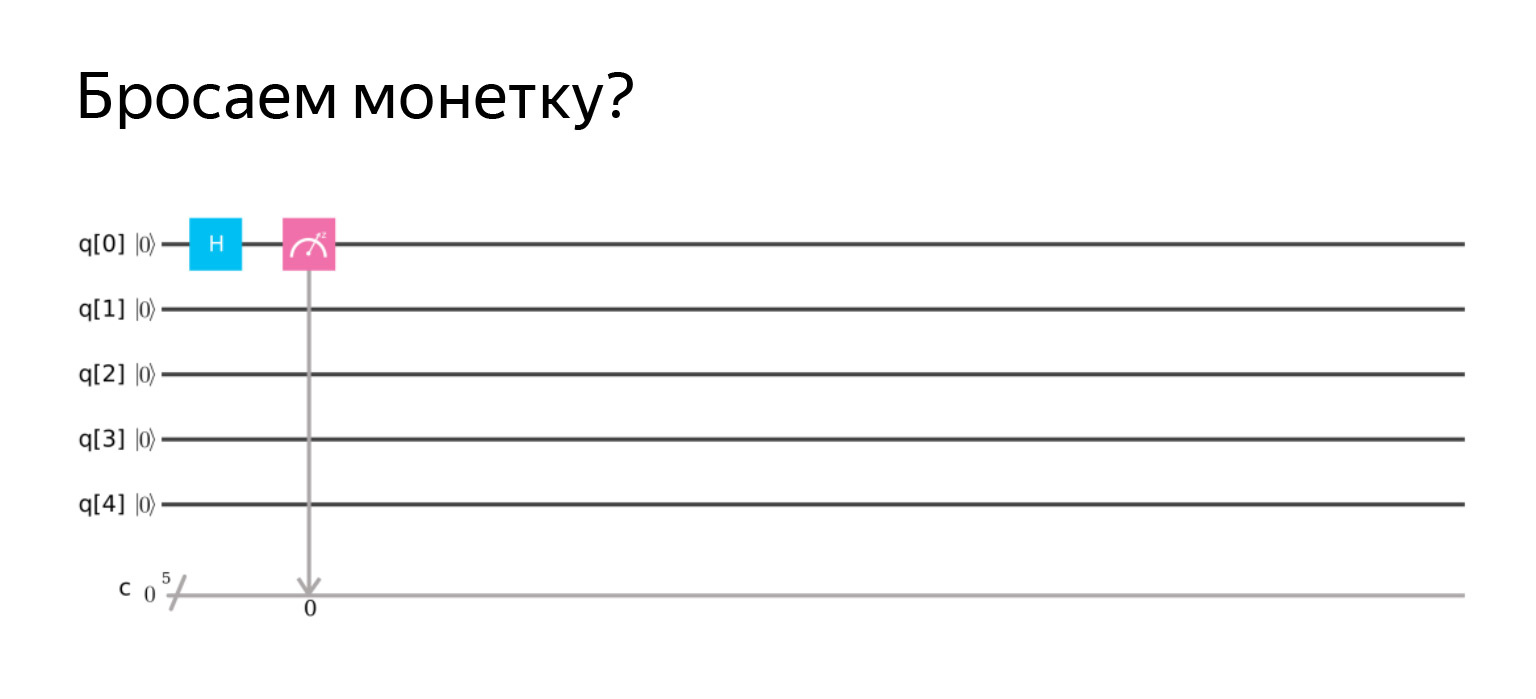
Easy to check, but we certainly won't. Let's draw a diagram. Operator H in honor of Hadamard.
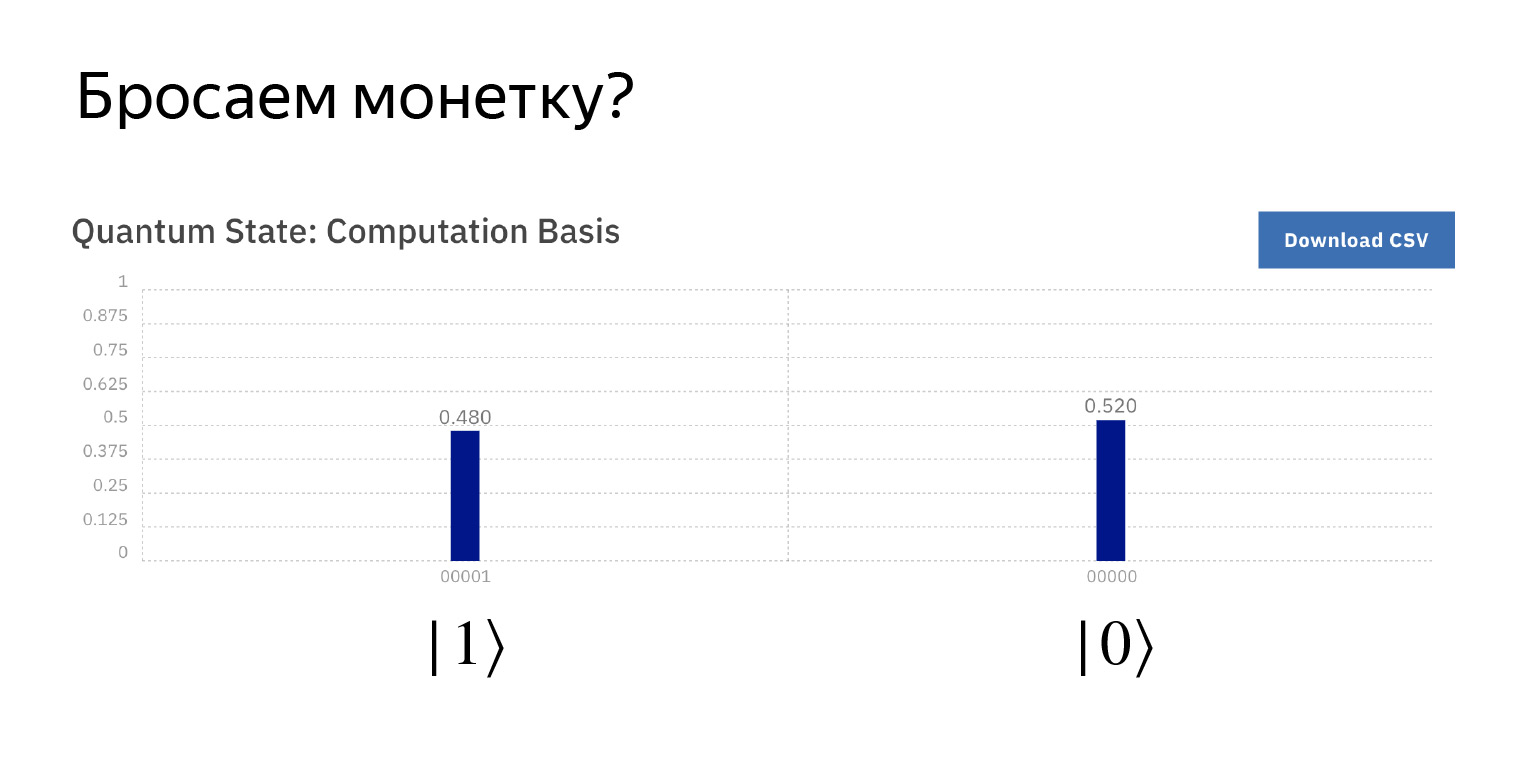
Let's measure and get approximately what we expect. With a probability of ½, zero and one. A little more, a little less, but that's how it works.
Here's the Python code, just to be there, we're at a Python conference.

There is such a superposition. We apply the Hadamard operator to it and measure.
But you can flip a coin twice, we are all used to this. If you flip a coin twice, nothing changes. Let's try to do this in the quantum case.

We apply the Hadamard operator two times in a row and we always get a zero.

That is, if you flip a quantum coin twice, you will always get a zero, because the Hadamard operator is inverse to itself. If you multiply by yourself, you always get one. Here's a thing.
So, you can do something with one qubit. Can be twisted, twisted and measured. Let's try adding more qubits. What are we used to doing in the classical world? Take and perform simple logical operations, "or" and "and".

In the quantum world, you cannot do this, because they are not completely reversible. That is, getting zero in the “and” operation, we can never know what the initial values were.
And in the quantum world, as I said, an operation is a unitary matrix that is always reversible. How, then, do you program at all? Everything we are used to is crumbling. But a new hero appears, this is the operator of the so-called controlled negation.

If we were writing in Python, it would look like this. If the first qubit is one, let's invert the second qubit. This is not a matrix, this is what the operator looks like. But in principle, what I said is written here. Where there is unity in the first qubit, the second is inverted.
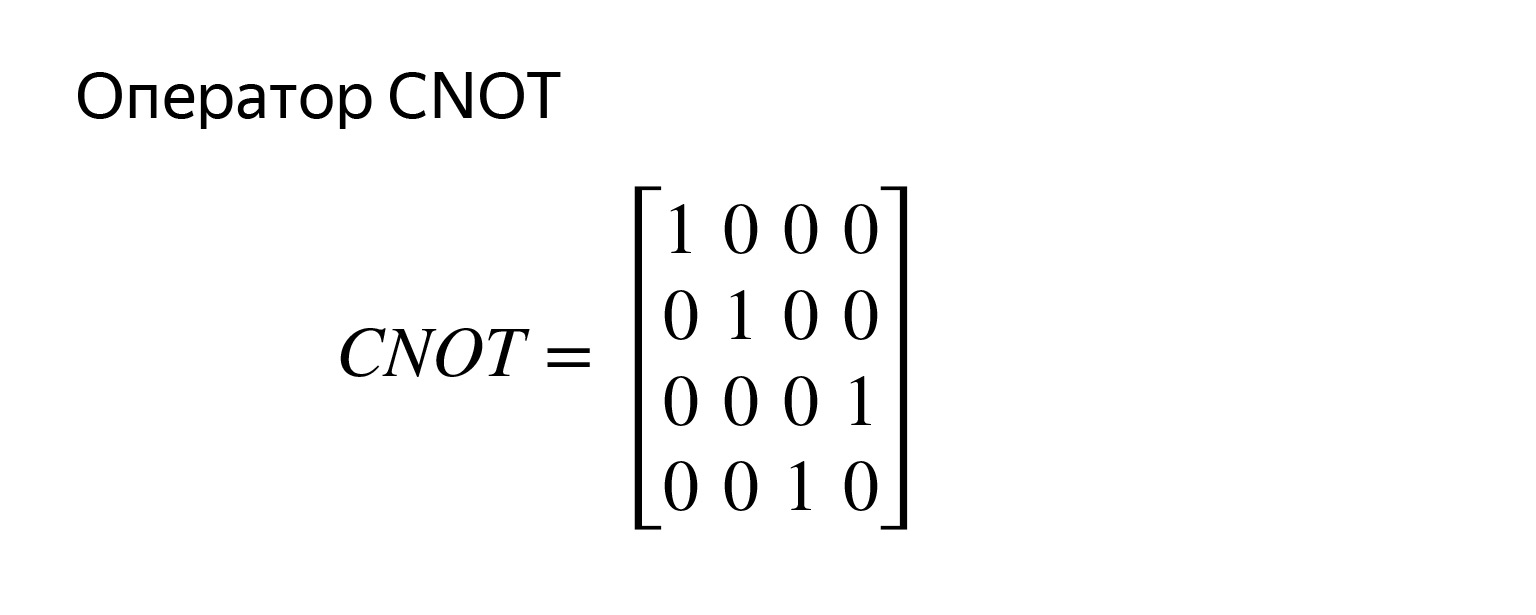
The matrix is already four by four. For two qubits, it looks like this. I'll leave the problem with an asterisk to multiply and see if this is true.

This thing can even be programmed. No rocket science. You just need to take, create a circuit with two qubits, with two classical ones, and do, not just CNOT, but CX, controlled negation.
Negation was the X operator, so in principle everything is logical. And you can draw a diagram. The scheme is as follows.
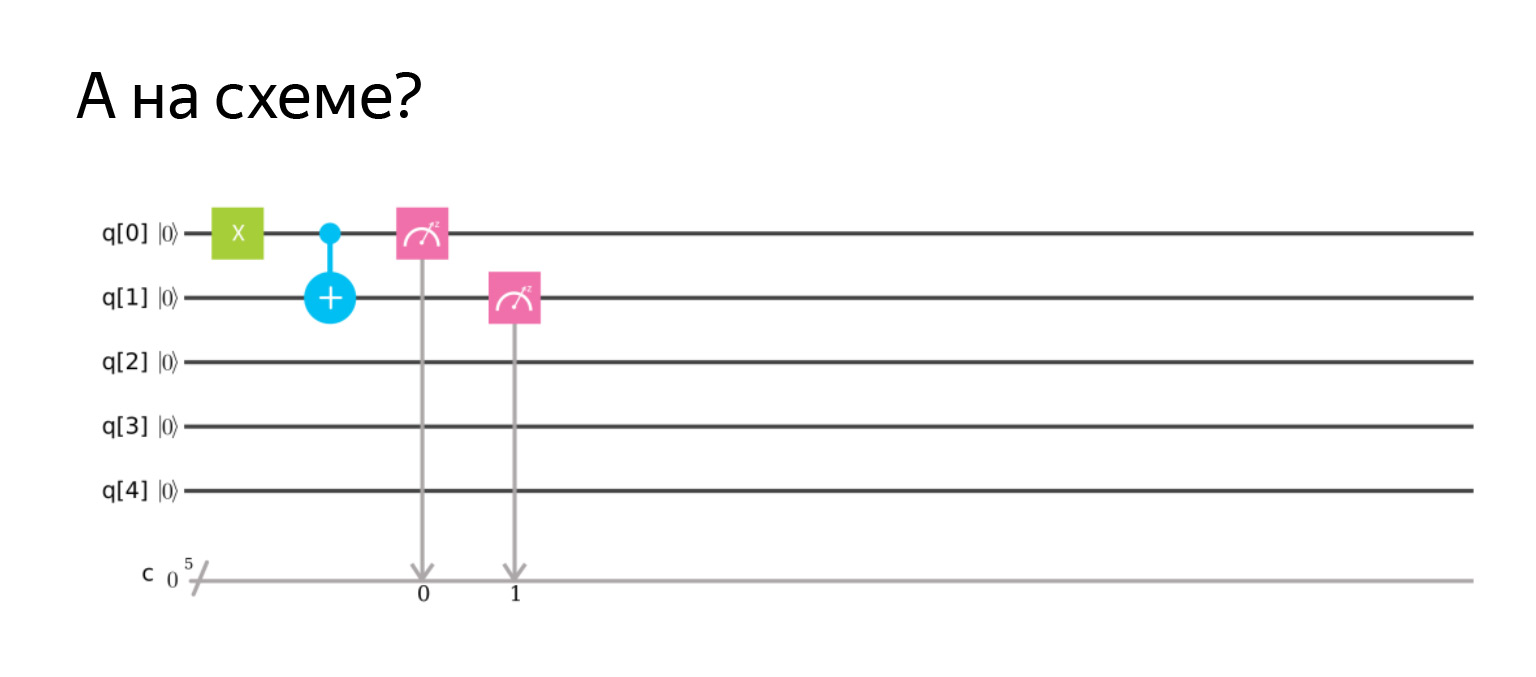
That is, controlled negation is such a plus on the qubit that we want to change. And the point, which is the control. Here, if the qubit is in unity, then we will change the second one.

Here I specifically first invert the first so that it is one, and then I measure both and get the result | 11⟩. Everything is as we expected.
But now is the time to use all our knowledge together.

Let's take all three or four operators that we know, and stick them into one scheme. That is, we apply the Hadamard operator to the first operator. Invert the second, then all together, do a controlled negation and measure.
Let's not run it yet, but try to guess what will happen.
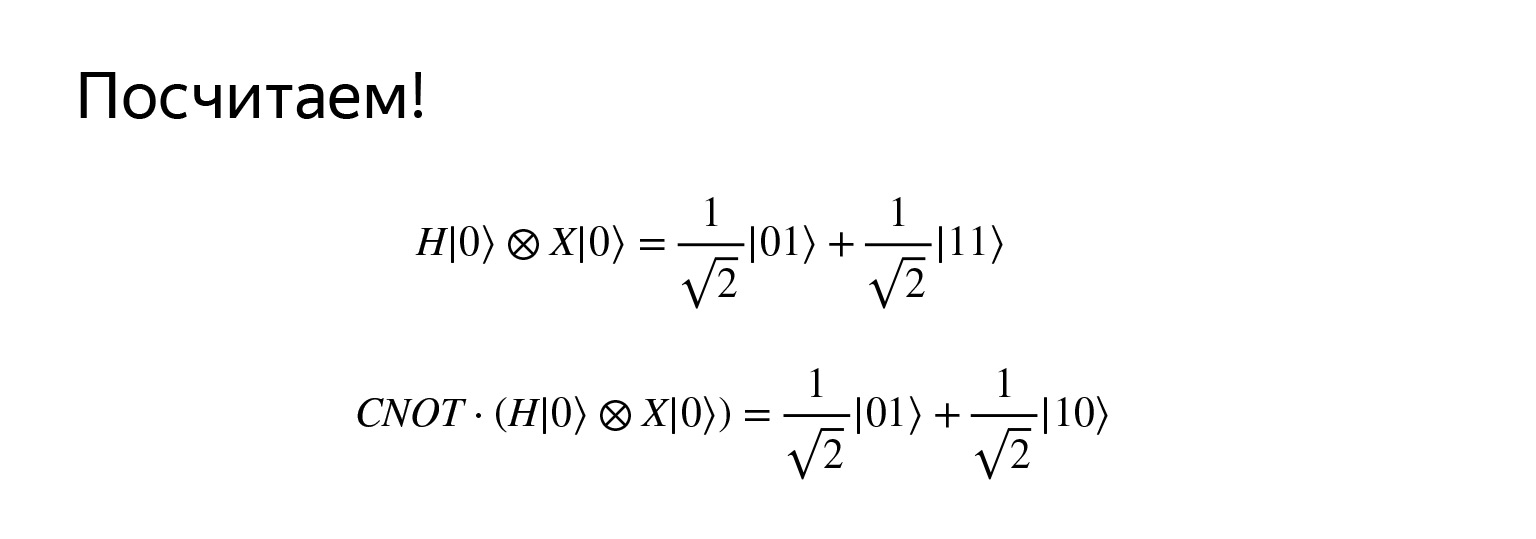
If we apply the Hadamard operator to the first qubit, and negate the second, then we get such a superposition. I don't want to waste time on checking now, it can be easily multiplied. But the position is very interesting. Firstly, it is very similar to uniform, and, secondly, now this state is called entangled, if we also take controlled negation.

The state is confusing. And why? Let's try to make a measurement. Look, if I measure the first qubit and I have it in state zero, then I can say that the second qubit is necessarily in state one.
That is, if I make such a transformation with my qubits, I give one qubit to my friend, he will fly to New York, and I measure the second qubit at myself, I will know exactly what state his qubit is in. This is called the effect of quantum entanglement or quantum connectedness. And this is the main mechanism by which quantum computing works. It will change, they are very rigidly connected, and during the measurement we can only get | 00⟩ or | 11⟩.
On this occasion, there is a very interesting illustration in favor of one scientist, Austrian, in my opinion,

The distraction was that he wore different socks all the time. And his colleagues joked about him: if he enters the room with one foot and we see that the sock is pink, then we can definitely say that the second sock is not pink. So it goes.
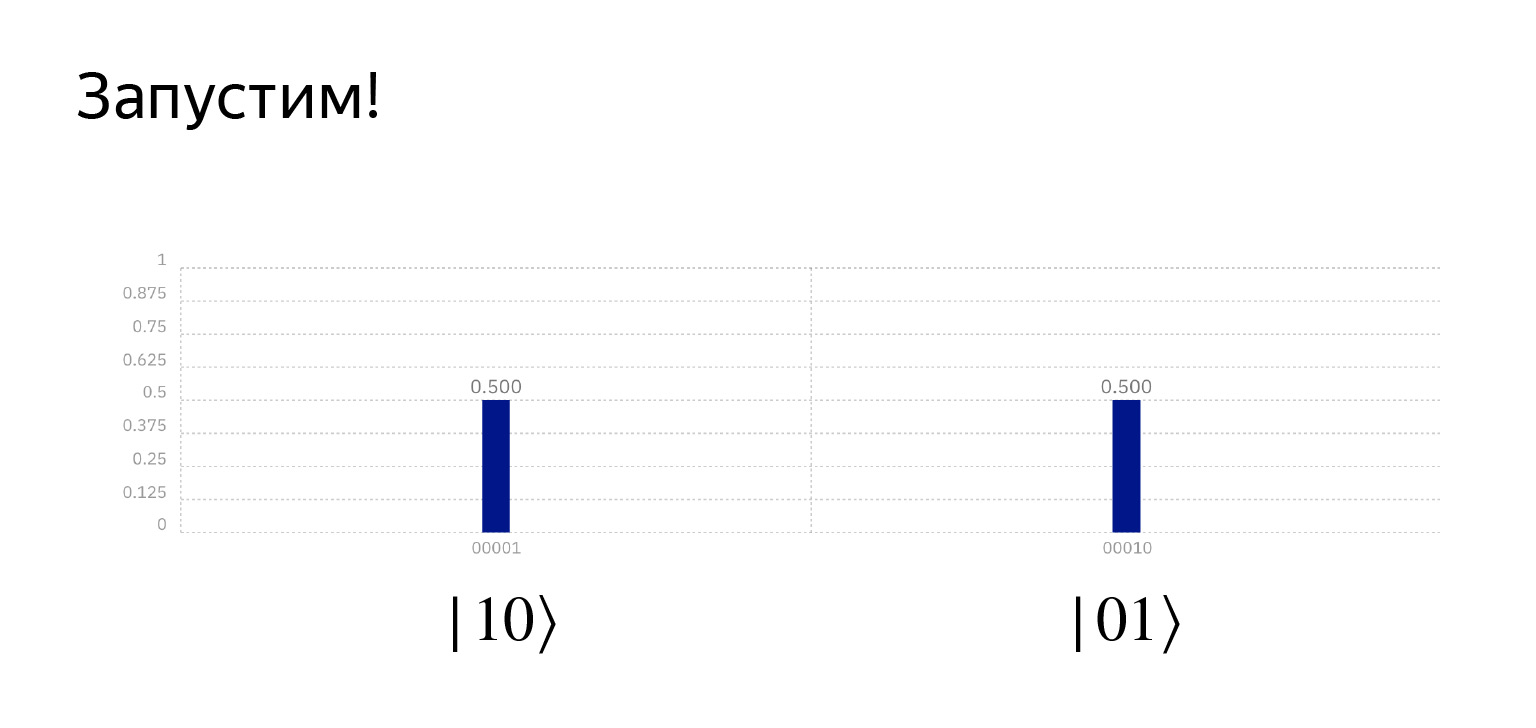
If we run this thing, we get exactly what we want. It's already quite funny here. The probability is exactly 0.5, but this is a coincidence.
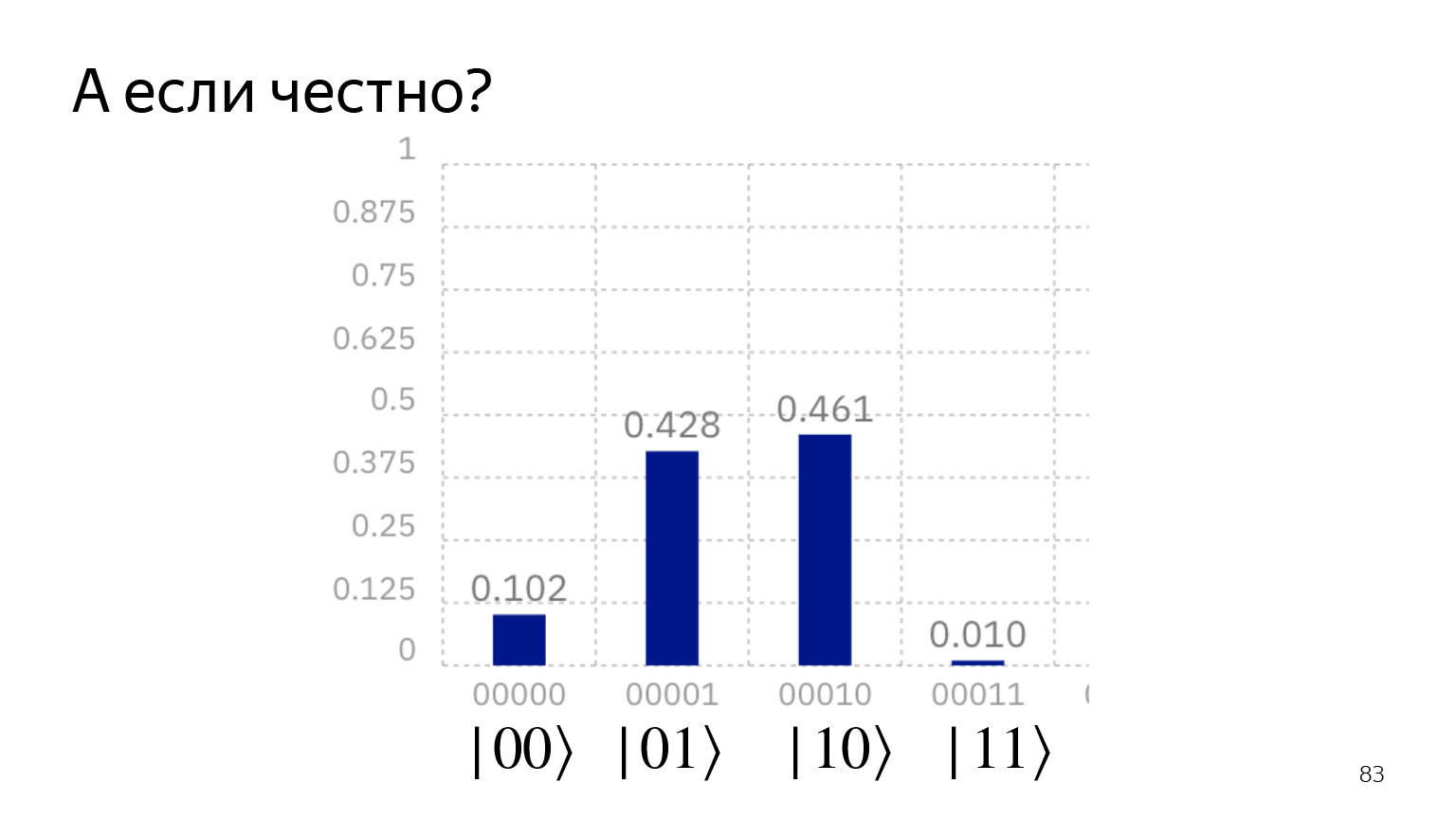
If we honestly run on a quantum computer, we get this picture. We seem to say: the state | 00⟩ can never be obtained and the state | 11⟩ can never be obtained. But it still works: the current state of technology is such that there are noises that cannot always be easily suppressed. And they are struggling with this.
But if you remember classical computer science, it's the same thing: error-correcting codes and all that. It's just that the qubit is too small for now to spend extra bits on error correction.
Now, as I promised, a few examples of algorithms. But these will be just unfounded examples without analysis of algorithms, so that you look, think, become interested.

The first algorithm is just related to Deutsch, which we talked about at the beginning. This is the Deutsch-Jozy algorithm. And he does the following. Imagine we have a Boolean function in n variables. And we know for sure that it is either constant or balanced. Balanced means that on exactly half of the arguments it is equal to zero, and on the other half - to one. Let's try to classically check whether it is constant or not.
To do this, we need to check at least half of all possible options: 2 n – 1 +1 option. The quantum algorithm allows you to do this in n calls to the function itself, in n calculations of the function itself. This is an exponentially lower number of hits.
The second example is probably well known to everyone, because of it they say that quantum computers will break all cryptography: we can factorize numbers quantum very quickly.

Difficulty estimates are given here and there is a fantastic example. In 2011, the number 15 was factored on a real computer. It took seven qubits.

But not everything is so bad. In case quantum computers reach the level at which you can break RSA, there is already post-quantum cryptography. It is built on learning with errors. This is when a small error is introduced into the problem so that it is very difficult to find an answer. Usually these are some kind of equations or a system of equations. Here's an example of the algorithm. Anyone who wants to can read in more detail.
Most interesting: the New Hope algorithm is based on this thing , the new hope of all mankind. In 2016, Chrome added support for this algorithm. There is a link to the blog here. This was not my idea, everything really is. The future is already here.
There are a few links at the end:
- , : Michael A.Nielsen and Isaac L. Chuang, «Quantum Computation and Quantum Information». , . .
- IBM Q: quantumexperience.ng.bluemix.net
- IBM Q User Guide: quantumexperience.ng.bluemix.net/proxy/tutorial/full-user-guide/introduction.html
- Qiskit: qiskit.org
- :
nplus1.ru/material/2017/06/07/quantumcomputers
nplus1.ru/news/2017/05/26/quantum-blockchain
This is more or less all. I just want to add that about 50 years ago, when Deutsch started doing quantum information science, computers were big. They were made by several companies. They were about the size of a wardrobe. And now, roughly the same companies make large quantum computers. And, of course, we do not know what will happen in 50 years.
If you try to type in your favorite search engine, then today you can find vacancies for a quantum programmer. Sure, there is more research out there, but nonetheless. Thank.