
This post is an adapted version of my two short video lectures “ Floating Rates and Benchmarks ” and “ Interest Swaps ” as part of the Finmath for Fintech course.
#1. Floating rates and benchmarks
Let's start with the main question: where do the banks get their money from? The answer lies on the surface: they borrow from other banks. This is called the interbank lending market or simply the interbank market . Large organizations give large sums of money, as a rule, for a short time - one day, one week, one month. Now let's imagine that you are in a large investment bank, for example, in London. At what percentage could you borrow today?
This is the question the British Bankers' Association began to ask about 30 years ago. They began collecting responses from key players, sorting them from smallest to largest, discarding margins, and counting the average. This is called LIBOR - The London Inter-bank Offered Rate. LIBOR is published in five currencies (euro, pound sterling, dollar, Swiss franc and yen) and seven tenors (by the way, in this case the tenor is not a voice in an opera, but such a time period) - one day, seven days, one month , two months, three months, six months and twelve months. Seven tenors are like seven days of the week. In total, we get 35 values every working day.
LIBOR , . , , LIBOR , .
LIBOR is also called a benchmark . As we know, a benchmark is something of a reference. In this case, the benchmark is the interest rate, which reflects the market sentiment, the current economic situation and other factors.
In 2018, LIBOR and a similar benchmark EURIBOR were awarded contracts totaling over $ 370 trillion. Agree, a sum with 13 zeros is a lot. We will look at what these contracts are a little later, but now let's look at EURIBOR.
I think you have already guessed that this is The Euro Interbank Offered Rate - the rate that is formed in the euro zone. Here attentive readers will ask: "Is there a difference between the euro rate in LIBOR and the euro rate in EURIBOR?" Of course, there are differences. Let's take a look at the illustration.
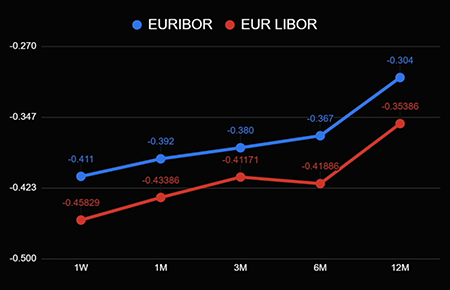
The graph shows that the curves are similar, but still different. This is not a random effect of one day, but a fundamental difference in the two rates that form in the two markets.
Let's now fast forward about 10 thousand kilometers to the east and find ourselves in the city of Tokyo. There the rate is formed, which is called TIBOR - Tokyo Inter-bank Offered Rate . Again we can compare LIBOR for yen and TIBOR for yen and see if they are different.
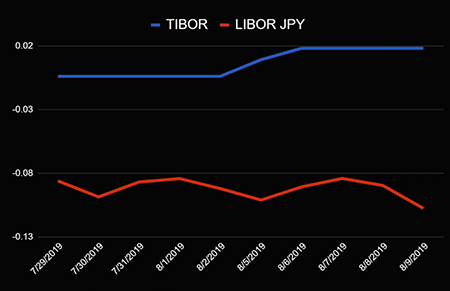
What conclusion do we draw from what we have seen? Each market publishes its own rate: in London it has its own, in the European zone it has its own, in Japan it also has its own. But let's jump back to London. It turns out that there is another rate there called SONIA (Sterling Overnight Interbank Average Rate)... It shows the average overnight lending rate in the interbank pound sterling market. Remember that LIBOR also has an overnight rate. Let's compare them on the graph.
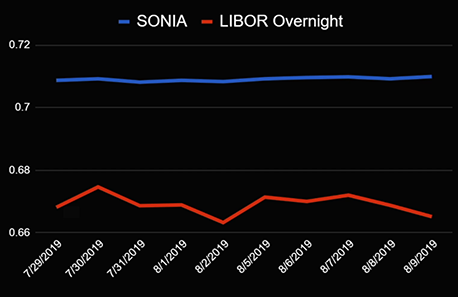
These are bets that are published in the same city for one currency, one tenor. But they are different! What is the reason?
LIBOR is a legendary interest rate. It is known not only for the fact that a huge number of contracts are tied to it (if you remember, this is an amount with 13 zeros), but also for the facts of benchmark manipulation. It became known that since 2008 the members of the LIBOR panel, that is, the banks that took part in the survey and provided the regulator with values for averaging and publication, deliberately overestimated or lowered the rate. The scandal erupted in 2012 and ended in multimillion-dollar fines for many banks (some fines reached one billion euros). The market realized that something needed to be done with LIBOR.
Protection against outside influence and LIBOR alternatives
The first thing that was changed was the calculation methodology. Before the scandal, LIBOR was considered simply as the arithmetic mean. Imagine that I want to somehow influence LIBOR. 16 banks are participating in the survey, which means that the four largest and four smallest values will be discarded, and the average will be calculated for the remaining eight. If I change my "fair" LIBOR value by + 0.08% and the sent value does not fall into the 25% of the largest and 25% of the smallest, then the official LIBOR value changes by + 0.08% / 8 = +0.01 %.
After the discovered manipulations, the rate was considered differently. The so-called waterfall-model appeared, which includes three layers. On the first layer, you account for your transactions - Level 1: Transaction Based. On the next layer, you take into account the market movement and historical transactions - Level 2: Transaction Derived. And only on the third layer you can add your expert judgment - Level 3 Expert Judgment. So LIBOR began to be considered differently, and the market started thinking about alternatives.
SONIA - the overnight rate for the pound sterling - is just such an alternative. It differs in the calculation method.
SONIA is the average for completed transactions in the interbank market, that is, firstly, it takes into account all market participants, and secondly, it is based on transactions, and not on expert estimates. Thus, this is a more objective assessment of the market. In addition, it is resistant to the manipulations described above.
The analogue of SONIA in the Eurozone is EURONIA, and in Russia - RUONIA. The analogue of LIBOR in Russia is MosPrime Rate - if you are interested, then using this value you can find out at what interest rate banks lend in Moscow.
Subtotals
So, we learned that there is an interbank market in which banks lend money to each other. Usually this money is given at a floating interest rate. These rates are new every day, and we call some benchmarks benchmarks - LIBOR, TIBOR, EURIBOR, MosPrime Rate and others. These benchmark interest rates differ in where they are generated (which country, in which city) and how they are calculated (for example, LIBOR is calculated in London by a survey of key market participants, and the EURONIA or RUONIA rate is calculated as the average of all transactions for a certain day). LIBOR and EURIBOR still have a huge number of contracts (more than 370 trillion last year alone). What these contracts are, read below.
# 2. Interest rate swaps
So we have two worlds. The first is the banking world, which operates at floating rates. The second is the non-banking world, which lives at fixed rates. Agree, if you come to the bank and ask: "At what percentage are you willing to place my money?", - you will be answered: "LIBOR + 50 bps (basis points)". Is it a lot or a little? If I were a banker and they told me that my money would be placed at LIBOR + 50 basis points, I would say: “Yes, we take it, now and as much as possible - this is very profitable”. But for you this does not mean anything, it is much clearer for you to hear: "Three percent." Obviously, banks have both individuals who understand 3% and clients who understand the expression "LIBOR + 50 bps".
, , interest rate swap (IRS). - .
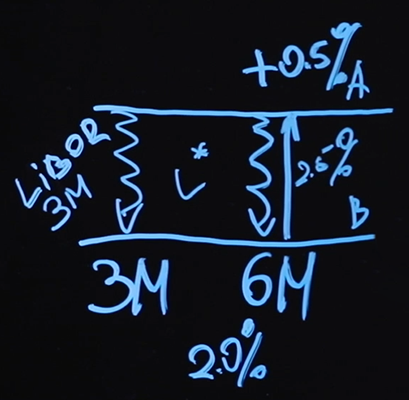
Let's see how the contract works. The contract is concluded between the two parties - side A and side B. Side A pays floating leg, Side B pays fixed leg. How often they do this depends on the parameters of the contract.
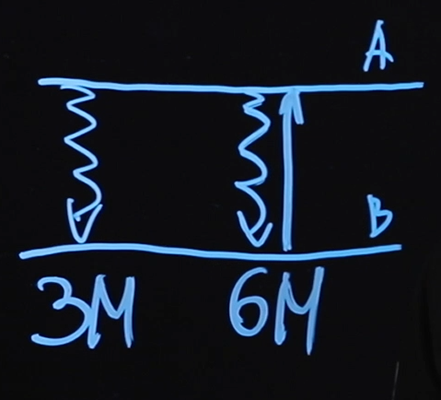
Our figure shows that every three months, side A will pay a floating "leg" to side B, and every six months, side B will pay a fixed "leg" to side A. The price of this fixed "leg", that is, how much interest it will be ( say 2.5%) - this will be the price of the interest rate swap.
What is happening on these floating "legs"? Here LIBOR is paid, most likely three months.

The first floating payment will be made in three months at today's LIBOR rate. After three months, the new LIBOR value will be known - this value will determine how much will be paid at the point six months, and so on.
Who will be in the black as a result? Let's say that on a floating leg we pay 2.2% first, and then 2.6%, and back on a fixed leg we get 2.5%, in total we get + 0.1% * N = - (2, 2% + 2.6%) / 2 * N + 2.5% * N, where N is the contract amount. A contract with such a payment scheme is called a vanilla swap (which, as you can imagine, has nothing to do with vanilla being used as a spice).
How many contracts of this type are being executed? According to statistics, in the first half of 2019, there were approximately 969,915 transactions totaling $ 38 trillion. That is, the volume of one transaction is $ 81 million, which, you see, is impressive.
Now let's move on to an interesting question like price. How much does such a contract cost? We call this Fair Price. The price is “fair”, because at the time of the transaction, the floating and fixed legs are the same.
Consider a trivial case with three payments: two floating every 6 months and one fixed every 12 months. Of course, real contracts are much more complicated than our scheme and usually consist of dozens of payments.
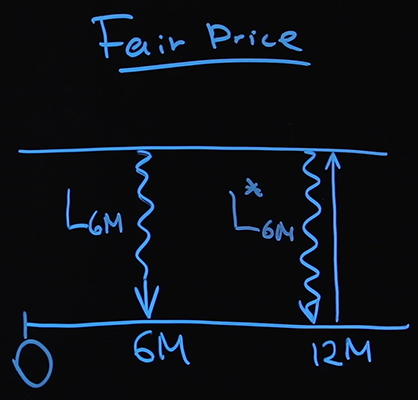
Let us recall where the floating payments values come from. So, we agreed on the contract today. We open the page where the LIBOR values are published, look at them. Let's say today LIBOR 6M L 6M = 2.2% - now we know exactly how much money one party will pay the other in six months. After six months, we will look again at LIBOR 6M - L * 6M . On a fixed leg, a certain percentage of P will be paid, which we will now calculate.
Recall that at the time of the transaction, both parties believe that there is no difference whether you receive two floating payments or one fixed. This means the following:
PV Fixed = PV Float
Let's write down PV (Present Value) for fixed and floating legs. The interest rate is multiplied by the contract amount N and multiplied by the discount factor at the point of 12 months.
PV Fixed = P * N * D 12m
Now let's write down PV Float . The difference will be in one term.
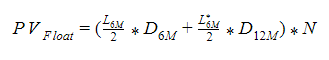
Why is LIBOR 6M divided by two? LIBOR is indicated in annual percentage, in our example the floating “leg” is paid every six months - it is logical that the annual rate should be divided by two.
It is not hard to find the meaning of "fair price".
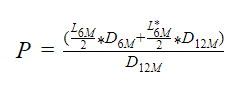
We need to know the LIBOR value somehow. We can look at the current value on the website, but where can we get the value of this parameter in six months? I write down the discount factors separately, without describing them through a well-known formula. I would like to draw a clear line between the LIBOR values that floating payments depend on and how we calculate the discount factor. Two curves are needed: a curve for LIBOR and a curve for discounting. In many textbooks you will come across phrases such as, for example, “We will discount by LIBOR” or “The discount factor is equal to… (some expression with LIBOR)”. What's the catch? In addition to the simplest vanilla swaps (by the way, the answer to the question why they are "vanilla" sounds like "Because there is nothing simpler than vanilla ice cream"), where on the one hand there is a floating "leg", on the other hand is fixed,there are swaps where the parties exchange only floating legs. For example, there is side A and side B. One pays LIBOR, the other - EURIBOR. This contract is called floating-floating interest rate swap.

It is clear that LIBOR should be in euros (by the way, there are contracts where one party pays LIBOR USD, and the other - LIBOR EUR - this is a cross-currency basis swap). If we follow the recommendations of the textbook and use the LIBOR discount factor, then in fact we have two rates that are identical in meaning. One is floating, which is being formed in London, the other is floating, which is being formed in the Eurozone. And why we should trust LIBOR more than EURIBOR is not very clear. By the way, in this case, the swap price will be the small percentage that we add to EURIBOR.

In this case, it becomes clear that it is not very correct to use any floating interest rate as a benchmark and then discount with it. Therefore, the following problem arises: for this particular swap, you need to calculate the LIBOR curve, EURIBOR curve and find the discount curve. The discount curve is the curve along which you will calculate discount factors to transfer payments from the future to the present.
How do you calculate the "fair price" for the Floating-Floating IRS? The approach is exactly the same. On the one hand, we have LIBOR divided by four (because three months is a quarter of the annual rate), which needs to be multiplied by the discount factor. This will be equal to the value of EURIBOR plus the same price P divided by four, all multiplied by the discount factor. Summation is made for all payments.
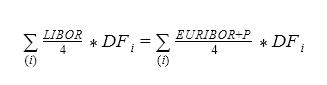
From this equation it is easy to find P, which is the "fair price" of the Floating-Floating IRS.
Why is this example interesting? He tells us that we need three curves: the LIBOR curve, the EURIBOR curve and the discount curve. The basic methods of plotting curves are the same, we will look at them with the example of a discount curve a little later. In the meantime, let's summarize.
Swap totals
We learned what an interest rate swap is. It is a product in which two parties are involved: one pays a fixed leg, the other a floating one. This is the easiest vanilla swap. There are also situations where both parties pay floating "legs" (Floating-Floating swap).
More than half a million transactions were concluded with the simplest vanilla swaps alone in early 2020. On average, the volume of each transaction is almost one hundred million dollars. We also learned how to calculate the "fair price" of a swap. We calculated it on the assumption that the PV of the floating leg is the same as the PV of the fixed leg, and we called this price fair, since it suits all parties to the transaction. Using the example of Floating-Floating swaps, we realized that sometimes we need to build several curves: curves for floating rates and a curve for discounting. We will talk about how to build a discount curve in the next part.
I hope that now you no longer "float" in the topic of floating interest rates and you can find vanilla among interest rate swaps.
Other articles in this series :
-Value of money, types of interest, discounting and forward rates. Educational program for a geek, Part 1
- Bonds: coupon and zero coupon, yield calculation. Educational program for a geek, Part 2
- Bonds: risk assessment and examples of use. Educational program for a geek, Part 3