
Optimization in business in the overwhelming majority of cases is associated with the use of the linear programming method. The method is fairly straightforward. In addition, there is a theorem on the existence and uniqueness of the solution.
However, in practice, everything is not entirely simple.
The first problem is the nonlinearity of real world conditions. In order for the linear programming method to be applicable, they must be linearized. There are ways to plausibly set nonlinearity through linear equations and inequalities by introducing new variables, setting weight coefficients, etc. When solving production problems in this case, it is necessary to operate with a large number of variables and, accordingly, equations (inequalities).
In the theory of solving extremal problems, there is a theorem on the stability of solutions to linear programming problems. According to it, the solution is stable only if the domain of the problem is convex. With a large number of variables and inequalities, it is not possible to establish whether the domain of the problem is convex. Moreover, the probability of non-convexity is high.
If the problem is not stable, then depending on the starting point of traversing the vertices, different results will be obtained.
Second problem- restriction of the variable from below (x> h> 0). Any implementation of a linear programming method will always provide a non-zero x value. If x is exactly equal to h, then this means that the value of the variable x should essentially be zero. In practice, such “fictitious” volumes (method kurtosis) are scattered over “meaningful” variables. The consequence of this practice is the erosion of the concept of an optimal solution, which is especially important if such a solution is one of many in the decision chain.
The third problem is managerial. The linear programming method gives only one result. And how to look at results that are close to optimal? For example, in the resulting solution, the vendor rating is poor. How to understand if there are close solutions, but for reliable suppliers.
Transport task
The example corresponds to a transport linear programming problem.
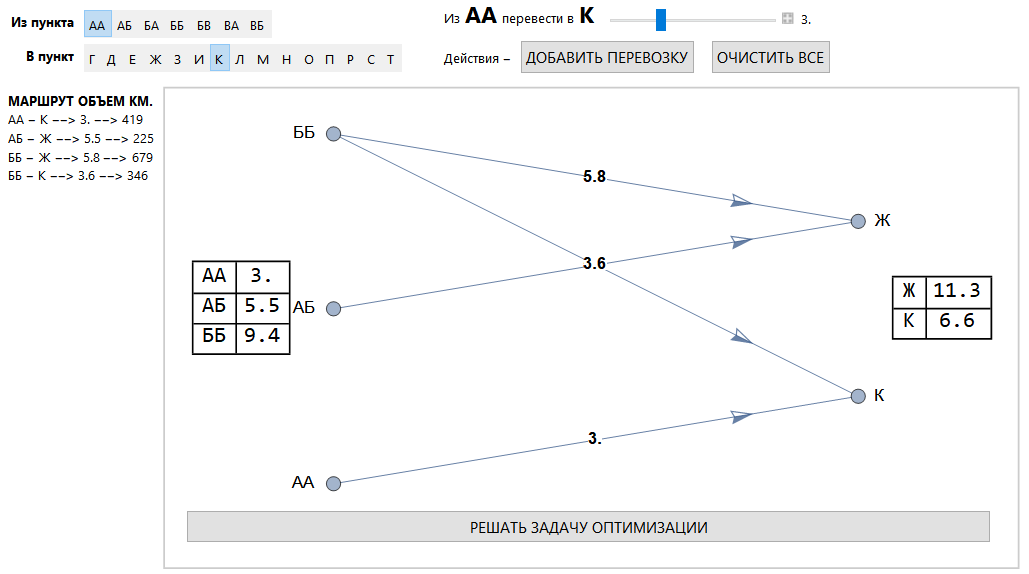
There are 5 carriers (the task was set for the transportation of coal), which have two tariff calculations. Tariff boundaries and tariffs themselves can be changed (they are set parametrically).

Transportation is specified as point-to-point (according to the accepted method for coal transportation) and volume.
General view of the interface.

Transportation assignment area.
Cluster solution method
Instead of one linear programming problem, a cluster of problems is solved, the number of which corresponds to all possible combinations of tariffs. In the above shipment, there are 127 of them (second value in the top left rectangle).

The optimal solutions are selected from the set of the remaining correct problems. Each task provides an optimal solution for a specific combination of tariffs. The solutions presented above constitute a certain range of maximums.
Why the cluster method is good:
- there is an understanding of the stability of the solution.
- there are no “fictitious” volumes for variables bounded from below, since there will be another combination where such a condition is absent (since such a variable is absent).
- subjective conditions (ratings, preferences) can be introduced using the standard linear programming method.
With a larger number of shipments, we have the following picture (fragment).
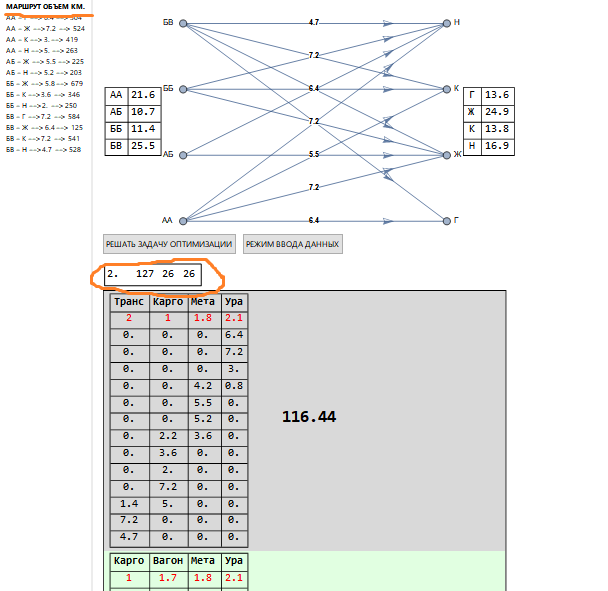
In the upper left corner, in the rectangle above the solutions (highlighted in orange), other values are indicated than before: 127 - combinations (as before, which is related to the structure of tariff scales), 26 - corresponds to the number of correct problems remaining that are being solved. The tariff used is indicated in red under the name of the carrier, and the transportation columns correspond to the list of routes (underlined orange)
It is important to note that the method used allows you to understand the result, evaluate similar solutions and use your professional experience when choosing alternatives, taking into account the intricacies of running a particular business.