Joshua Green and Andrew Lobb, bored in quarantine, figured out how to prove one of the variants of the rectangular peg theorem

Can all kinds of rectangles be found in a closed loop?
In mid-March, mathematicians Joshua Green and Andrew Lobb found themselves in a similar position - locked within four walls, trying to adapt to the growing coronavirus epidemic. They decided to deal with it by delving into their research.
“I think the pandemic was some kind of catalyst for this process,” said Greene, a professor at Boston College. "We decided that it would be better to put on some kind of joint work that can support us."
One of the problems the two friends decided to tackle was a variant of the geometric question that had remained unanswered for over a hundred years.
"This task is extremely simple to formulate and understand, but it is very difficult to solve," - saidElizabeth Denn of Washington and Lee University.
It all starts with a closed loop - any curved path that has the same beginning and end. The task that Green and Lobb have taken on essentially argues that in any such path there are sets of four points that make up the vertices of a rectangle of any given proportion.
And while this "rectangular peg problem" sounds like a question any high school student with a ruler and compass can handle, he has resisted the most persistent attempts of mathematicians for many decades. And when Green and Lobb took over, they had no reason to expect anything else.
Greene said that of all the difficult projects he worked on, "this one was the least promising in my opinion."
But the pandemic grew, and Green and Lobb, who work at Durham University in England and the Okinawa Institute of Science and Technology, respectively, had weekly Zoom conversations and quickly spawned several ideas. And then on May 19, when many parts of the world reopened, they published their decision .
Their final proof, which shows that rectangles can indeed be found, takes this problem to a completely different geometric level. And there this stubborn question gives in very easily.
"It's pretty weird," said Richard Schwartz of Brown University. "This idea was perfect for this task."
Rethinking rectangles
The problem of rectangular pegs is closely related to the question posed by the German mathematician Otto Töplitz in 1911. He predicted that on any closed curve you can find four points, connecting which you can get a square. This question of his about "square pegs" remains open.
“This is an old and frustrating task that cannot be hacked in any way,” Green said.
To understand the complexity of the problem, it is important to know the properties of the curves that are considered in the square peg problem - this is also important for the proof of Green and Lobb.
This couple solved the problem for closed curves, both "continuous" and "smooth". Continuity means no breaks. Smoothness means continuity and no corners. You are likely to draw a smooth, continuous curve if you sit down at your desk with paper and pencil. They are "easier to work with," Green said.
Smooth continuous curves are different from simply continuous, but not smooth curves, such as those involved in the Toeplitz conjecture of square pegs. Such a curve can have corners - points at which the curve suddenly deviates and goes in a different direction. One prime example of a curve with many angles is the snowflake-like fractal Koch curve., in fact, consisting of some corners. The Koch snowflake and other similar curves cannot be analyzed using algebraic methods, which makes them especially difficult to study.
"Some continuous [not smooth] curves are just disgusting," Denn said.
But nevertheless, the problem solved by Green and Lobb belongs to smooth and, therefore, continuous curves. And instead of figuring out whether there are always four points on such curves that form a square - for smooth continuous curves this issue was solved in 1929 - they studied something else: are there always four points on such curves that form a rectangle of any given proportions, i.e. with any aspect ratio. For a square, this ratio is 1: 1, for high-definition TVs - 16: 9.

The first major breakthrough in the rectangular peg problem came in evidence found in the late 1970s by Herbert Vaughn. It offered a new way of looking at the geometry of rectangles and provided several methods that were later used by other mathematicians, including Green and Lobb.
“Everyone knows this proof,” Green said. "It's almost folkloric, you learn about such things by discussing everything at the dinner table."
Instead of imagining a rectangle as four connected points, Vaughn envisioned it as two pairs of points that are in a certain relationship with each other.

Imagine a rectangle with vertices ABCD. In it, the distance between the points AC (on the diagonal) is equal to the distance between the points BD (on the other diagonal). Also, these diagonals intersect exactly in the middle.
Therefore, when searching for rectangles on a closed loop, you can search for pairs of points lying at the ends of the same line segments intersecting in the middle. To find them, it's important to come up with a systematic way to describe them.
To understand what this means, let's start with something simpler. Take the number line. Let's choose two points on it - let's say numbers 7 and 8 - and construct them as one point on the numerical plane (7, 8). We can also build points that are a pair of identical numbers (7, 7). Now let's consider all possible pairs of numbers that can be found on the number line (and there are many of them!). If we build all pairs of such numbers, then we will fill the entire number plane. Another way to express this is to say that the number plane "parameterizes", that is, it collects all pairs of numbers on the number line in an ordered manner.
Vaughn did something similar with pairs of points on a closed curve. It, like the number line, one-dimensional, only closes in on itself. He realized that if you take pairs of points with a curve, and build a figure from them (and it doesn't matter which one is the x coordinate and which one is the y), then the plane will not work. Instead, you get an unexpected figure - a Mobius strip , a two-dimensional surface with only one side.

And in a sense, this is quite logical. To understand why - select a pair of points on the curve, and name them x and y. Now move from x to y, moving along one part of the curve, and simultaneously - from y to x, moving along the opposite. In the process, you will go through all pairs of points on the curve, starting and ending on an unordered pair (x, y). But this will return you to the very beginning - only the final sequence of points will be opposite to the initial one. A loop of disordered points changing orientation to the opposite is the essence of the Möbius strip.
This ribbon gives mathematicians a new object that can be analyzed as part of the rectangular peg problem. Vaughn used this fact to prove that on any curve there is at least one set of four points that form a square.
Four-dimensional answers
Green and Lobb's proof is based on Vaughn's work. However, it also combines several additional findings, some of which are relatively recent. Final proof is like a precise instrument, the desired outcome of which relies on a carefully considered combination of ideas.
One of the first main ingredients of their proof came in November 2019, when Princeton University PhD student Cole Hugelmeyer published the paperdemonstrating a new way of analyzing the Möbius strip used by Vaughn. It used a mathematical process known as nesting, which is when we take an object and project it onto geometric space. As a result, Green and Lobb took Hugelmeyer's technique and transferred it to another geometric space. But to understand what they did, you first need to understand what he did.
Here's a simple example of nesting.
Let's start with a one-dimensional line. Each point of a straight line is defined by a single number. Now we will embed this line in two-dimensional space - that is, we will draw it on a plane.
After embedding a straight line on the xy plane, each point in it is already determined by two numbers - the x and y coordinates, which describe where exactly the point is on the plane. You can now analyze the line using 2D geometry techniques.
Hugelmeier's idea was to take something like a Möbius strip, but embed it in a 4-space, where the properties of 4-dimensional geometry will allow you to prove the results you want.
“Basically, you have a Mobius strip, and you need to assign four coordinates to each point. It will be something like the address of a point in four-dimensional space, ”said Lobb.
Hugelmeyer assigned these addresses in such a way that it was easier to arrive at the main goal, finding rectangles on a curve. We can say that he assigned to each point on the curve something like a postal address - state, city, street name and house number.
To do this, he started from a specific point on the Mobius strip and took the two points on the original closed curve that she denoted. Then he found the midpoint of the line segment connecting these points, and determined its x and y coordinates. We got the first two values of the four-dimensional address (state and city).
He then measured the distance between the two original points on the curve. This length became the third value of the four-dimensional address (street name). Finally, he calculated the angle between the line segment connecting the two original points and the x-axis. This angle became the fourth value of the four-dimensional address (house number). These four values tell you everything about a pair of points on the curve.

This exercise sounds challenging enough, but it paid off quickly. Hugelmeyer took the attached Mobius strip and turned it around. The rotated Mobius strip has moved relative to its original position, and the two copies of the strip intersect. Since the turn took place in four-dimensional space, the self-intersection shape of the Möbius strip is difficult to imagine - but it is easy to describe mathematically.
This intersection was of great importance. When two copies of the Mobius strip are superimposed on each other, two pairs of points can be found on the original closed curve, forming the four vertices of the rectangle.
Why?
First, remember that a rectangle can be represented as two pairs of points with a common center of intersection of segments of the same length connecting them. It is this information that is encoded in the first three values of the four-dimensional address assigned to each point of the nested Möbius strip.
Secondly, in four-dimensional space, you can unfold the Mobius strip in such a way as to change only one of the coordinates of each point in its four-dimensional address - the house number changes, but the street, city and state remain. As an example, remember that if you take a brick, position it in front of you, and then move it to the right, then only its x coordinate will change, but not y or z.
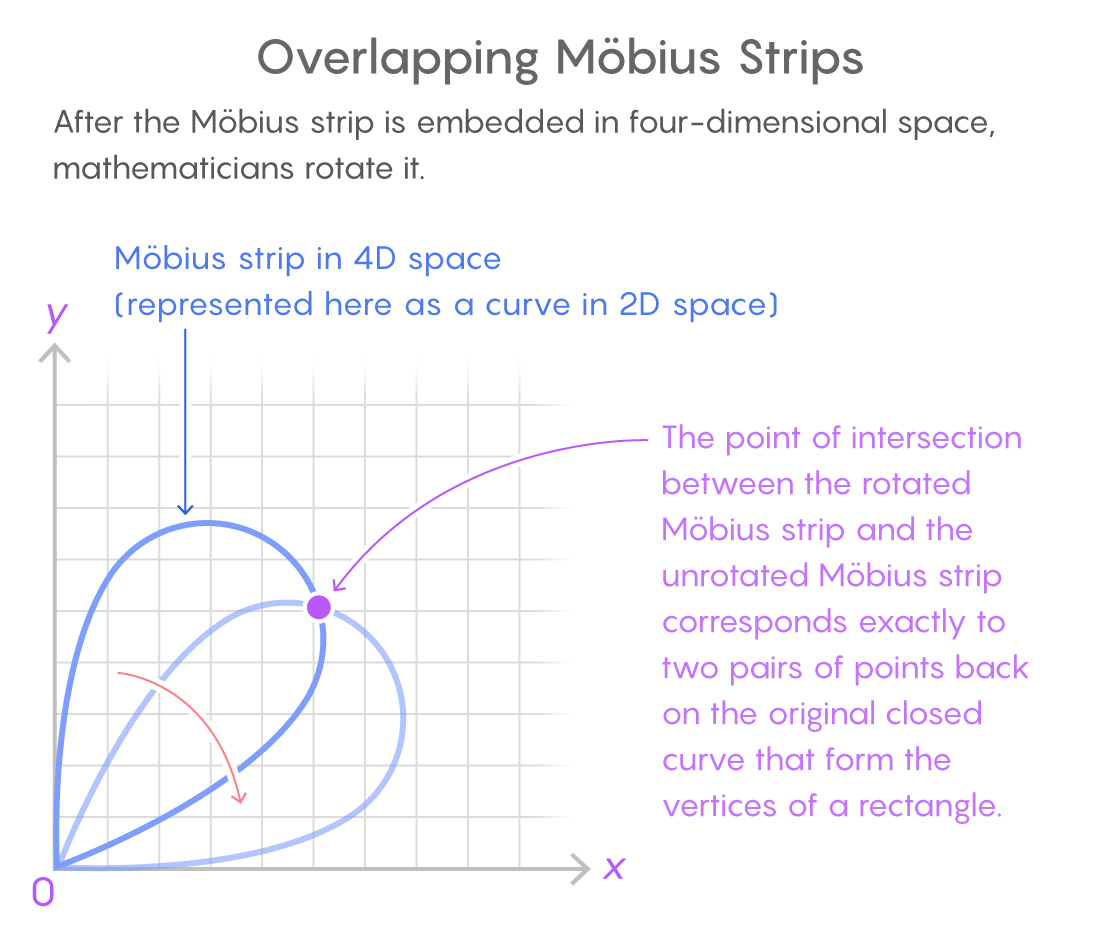
The Möbius strip in four-dimensional space is here indicated by a two-dimensional curve. The intersection point of the two copies corresponds to two pairs of points on the original closed curve that form a rectangle.
Hugelmeyer explained how to rotate the Mobius strip in four-dimensional space so that the two coordinates that indicate the midpoint of the lines connecting the pairs do not change - as do the coordinates that indicate the distance between pairs of points. Its rotation changed only the last coordinate - containing information about the angle at which the segment connecting the points is located.
As a result, the intersection of the rotated copy of the Möbius strip and its original exactly corresponded to two pairs of points located on a closed curve, having a common center (intersections of the segments connecting them) and located at the same distance from each other. That is, this intersection corresponded to the four vertices of the rectangle on the curve.
The strategy of using the intersection of two spaces to find the desired points has long been used in work on the problems of square and rectangular pegs.
"At the intersection of these spaces is the desired one," said Denn. "A lot of the evidence from the history of square pegs has this idea."
Hugelmeyer used an intersection strategy in a four-dimensional environment and got more than anyone before him could. The Mobius strip can be rotated any angle from 0 ° to 360 °, and he proved that a third of all these rotations result in the intersection of the original and the rotated copy. This is equivalent to stating that you can find rectangles on a closed curve with a third of all possible aspect ratios.
“Let's give credit to Cole for thinking about putting a Mobius strip in 4D space and using 4D techniques,” Green said.
At the same time, Hugelmeier's result turned out to be provocative: if four-dimensional space is so useful for working with this problem, why was it useful for only a third of all rectangles?
“After all, there has to be a way to get the remaining two-thirds,” Green said. - But how?"
Symplectic approach
Green and Lobb were interested in the problem of rectangular pegs even before the pandemic sent them home. In February, Lobb hosted a conference at the Okinawa Institute of Science and Technology , which Green also attended. The couple spent a couple of days talking about this task. After that, they discussed it for another week, along the way seeing the sights of Tokyo.
“We have not stopped discussing this issue,” Lobb said. "We went to restaurants, cafes, museums, and from time to time we had thoughts about this."
They continued their discussions even after they were locked in their homes. They hoped to prove that any rotation of the Mobius strip would give an intersection point - which is equivalent to finding rectangles of any proportion.
In mid-April, they formed a strategy. It meant embedding the tape in a special kind of four-dimensional space. Regular nesting implies that you place the desired object in any way. Imagine how many ways you can embed a one-dimensional closed curve in a two-dimensional plane - their number is infinite, as there are infinitely many ways in which you can place a thread tied in a loop on a table.
But let's say that the two-dimensional surface in which you nest the loop has its own structure. Imagine, for example, a map with arrows (or vectors) indicating to us in which direction and at what speed the wind blows on the surface of the Earth. Now you have a 2D surface with additional information, or structure, at each point.
Then you can introduce restrictions - a one-dimensional RFP must be put on the map so that it always follows the directions of the arrows on the map.
“You are limiting things so that the curve follows these vectors,” Schwartz said. And now you have fewer ways to place the curve.

Other geometric spaces may impose different constraints. Important for the work of Green and Lobb was the so-called. symplectic space .
This geometric concept first appeared in the 19th century when studying such physical systems as orbiting planets. The position of a planet moving in three-dimensional space is determined by three coordinates. But, as Irish mathematician William Rowan Hamilton observed, at each point of the planet's motion path, you can also place a vector denoting its momentum.
In the 1980s, Soviet and Russian mathematician Vladimir Igorevich Arnold developed the study of symplectic geometry . He realized that the geometric spaces of a symplectic structure, when rotated, intersect with themselves more often than spaces that do not have such a structure.
This was perfect for Green and Lobb, as they wanted to solve the rectangular peg problem for all proportions, proving that a rotated copy of a parametrizing Mobius strip also frequently intersects itself. So they started trying to embed a two-dimensional Möbius strip in a four-dimensional symplectic space. “A radically new idea was to approach this problem from the point of view of symplectic geometry,” said Green. "And that changed everything."
By the end of April, Green and Lobb determined that it was possible to embed a Mobius strip in a four-dimensional symplectic space so that it would come in line with its structure. After that, they could start using symplectic geometry tools, many of which are directly related to the question of self-intersections.
“If the Möbius strip can be made to follow symplectic rules, some of the symplectic theorems can be used,” Lobb said.
Green and Lobb were confident that they could improve Hugelmeyer's result - that is, prove that the intersection occurs not only at a third of all corners. This will mean that from the points of the curve it will be possible to make rectangles with more than a third of all possible proportions.
“When we got this idea, it became clear that something was going to happen,” Lobb said.
However, their results turned out to be more general, and appeared much faster than they expected. All thanks to a strange mathematical object - the Klein bottle , which in the context of symplectic geometry has one important property.
Klein bottle connection
The Klein bottle is a two-dimensional surface that looks like a modernist jug. It, like the Mobius strip, has only one surface, and it can be made by gluing two Mobius strips. Any Klein bottle that you can collect and place on your desk (as many mathematicians do) crosses over itself. It is impossible to put a Klein bottle in three-dimensional space so that it does not cross itself.
“The Klein bottle has to be a surface, but its handle needs to break through the bottle to go from outside to inside,” Schwartz said.
However, this is not necessarily the case. The Klein bottle can be nested in 4D space so that it does not intersect itself. The fourth dimension provides room for maneuver, and the Klein bottle can bypass itself. This can be compared to how if two people walk towards each other in a one-dimensional line, they cannot avoid a collision, but if they walk on a two-dimensional floor, they can easily turn away.

In May, Green and Lobb recalled one fact about the Klein bottle - it cannot be embedded in a four-dimensional symplectic space so that it does not intersect itself [from the work of another Russian mathematician, Vsevolod Viktorovich Shevchishinconcerning the Lagrangian embedding of the Klein bottle in four-dimensional space / approx. transl.]. In other words, there is no Klein bottle without self-intersection that satisfies all the requirements of a symplectic space. This fact became the key to the proof. “It was a magic wand,” Green said.
And that's why. Green and Lobb have already shown that it is possible to embed a Mobius strip in a four-dimensional symplectic space so that it satisfies his requirements. They only needed to figure out whether each turn of the Mobius strip intersects the original copy.
However, two intersecting Mobius strips are equivalent to a Klein bottle, which intersects itself in such a space. And if you rotate the Mobius strip so that the rotated copy does not intersect with the original, you get a Klein bottle that does not cross itself. But such a Klein bottle cannot exist in four-dimensional symplectic space. Therefore, any possible rotation of the nested Mobius strip must also intersect itself - that is, on each closed smooth curve, four points can be found that form a rectangle of any proportions.
The end of the proof hits the reader like an avalanche.
“It’s first set up, set up, set up, and then grunt, and the proof is ready,” Denn said.
Green and Lobb's proof is a good example of how solving a problem often relies on finding the right point of view. Generations of mathematicians have been unable to tackle this version of the rectangular peg problem because they have tried to solve it in more traditional geometric conditions. When Green and Lobb brought the problem to the symplectic world, it was easily solved.
“These problems, which emerged in the 1910s and 1920s, did not have a suitable platform to reflect on them,” Green said. "And now we are beginning to understand that they are, in fact, hidden incarnations of the phenomenon of symplecticity."