capable of performing millions of operations per second. And naturally, you can't do without simulation of the real or game world. One of the problems of computer modeling and simulation is to determine the collision of two objects, one of the solutions of which is realized by the theorem on the separating axis.

Note. The article will give an example with 2 parallelepipeds (hereinafter - cubes), but the idea for other convex objects will be preserved.
Note. All implementation will be done in Unity.
Act 0. General theory
First, you need to get acquainted with the " separating hyperplane theorem ". It will be the basis of the algorithm.
Theorem. Two convex geometries do not intersect if and only if there is a hyperplane between them that separates them. The axis orthogonal to the dividing
hyperplane is called the dividing axis, and the projections of the figures onto it do not intersect.
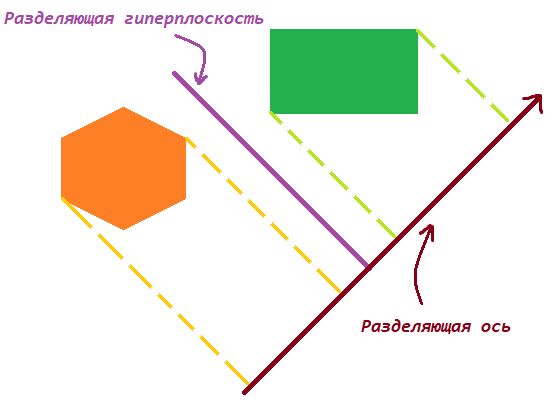
Dividing axis (2D case)
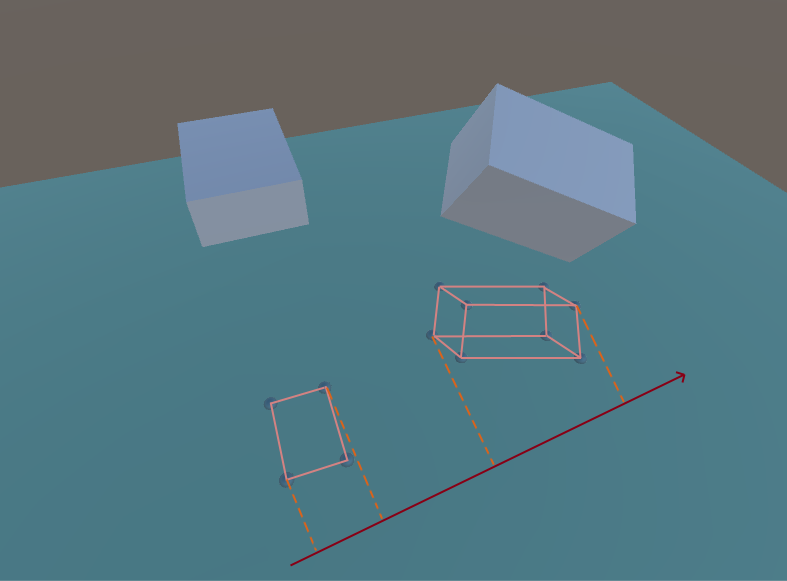
Dividing axis (3D case)
You may notice that the projections on the dividing axis do not intersect.
Property. The potential dividing axis will be in the following sets:
- Plane norms of each cube (red)
- Vector product of the edges of the cubes ,
where X is the edges of the first cube (green) and Y is the second (blue).

We can describe each cube with the following input data:
- Cube center coordinates
- Cube dimensions (height, width, depth)
- Quaternion of the cube
Let's create an additional class for this, instances of which will provide information about the cube.
public class Box
{
public Vector3 Center;
public Vector3 Size;
public Quaternion Quaternion;
public Box(Vector3 center, Vector3 size, Quaternion quaternion)
{
this.Center = center;
this.Size = size;
this.Quaternion = quaternion;
}
// ,
// GameObject
public Box(GameObject obj)
{
Center = obj.transform.position;
Size = obj.transform.lossyScale;
Quaternion = obj.transform.rotation;
}
}
Act 1. Quaternions
As is often the case, an object can rotate in space. In order to find the coordinates of the vertices, taking into account the rotation of the cube, you need to understand what a quaternion is.
Quaternion is a hypercomplex number that determines the rotation of an object in space.
The imaginary part (x, y, z) represents a vector that defines the direction of rotation. The
real part (w) defines the angle at which the rotation will be performed.
Its main difference from all the usual Euler angles is that it is enough for us to have one vector, which will determine the direction of rotation, than three linearly independent vectors that rotate the object in 3 subspaces.
I recommend two articles that go into more detail about quaternions:
One
Two
Now that we have a minimal understanding of quaternions, let's understand how to rotate a vector and describe the function of rotating a vector with a quaternion.
Vector rotation formula
Is the required vector
- original vector
- quaternion
- inverse quaternion
To begin with, let us give the concept of inverse quaternion in an orthonormal basis - it is a quaternion with an imaginary part of the opposite sign.
Let's count
Now we will write out the individual components and from this product we will collect a new quaternion
Let's count the rest, i.e. and get the desired vector.
Note. In order not to overload the calculations, we present only the imaginary (vector) part of this product. After all, it is she who characterizes the desired vector.
Let's collect the components of the vector
Thus, the required vector is obtained.Write the
code:
private static Vector3 QuanRotation(Vector3 v,Quaternion q)
{
float u0 = v.x * q.x + v.y * q.y + v.z * q.z;
float u1 = v.x * q.w - v.y * q.z + v.z * q.y;
float u2 = v.x * q.z + v.y * q.w - v.z * q.x;
float u3 = -v.x * q.y + v.y * q.x + v.z * q.w;
Quaternion M = new Quaternion(u1,u2,u3,u0);
Vector3 resultVector;
resultVector.x = q.w * M.x + q.x * M.w + q.y * M.z - q.z * M.y;
resultVector.y = q.w * M.y - q.x * M.z + q.y * M.w + q.z * M.x;
resultVector.z = q.w * M.z + q.x * M.y - q.y * M.x + q.z * M.w;
return resultVector;
}
Act 2. Finding the vertices of a cube
Knowing how to rotate a vector with a quaternion, it will not be difficult to find all the vertices of the cube.
Let's move on to the function of finding the vertices of a cube. Let's define the base variables.
private static Vector3[] GetPoint(Box box)
{
//
Vector3[] point = new Vector3[8];
//
//....
return point;
}
Next, you need to find a point (anchor point) from which it will be easiest to find other vertices.
Subtract half the cube dimension from the center coordinatewise, then add one cube dimension to the reference point.
//...
//
point[0] = box.Center - box.Size/2;
point[1] = point[0] + new Vector3(box.Size.x , 0, 0);
point[2] = point[0] + new Vector3(0, box.Size.y, 0);
point[3] = point[0] + new Vector3(0, 0, box.Size.z);
//
point[4] = box.Center + box.Size / 2;
point[5] = point[4] - new Vector3(box.Size.x, 0, 0);
point[6] = point[4] - new Vector3(0, box.Size.y, 0);
point[7] = point[4] - new Vector3(0, 0, box.Size.z);
//...
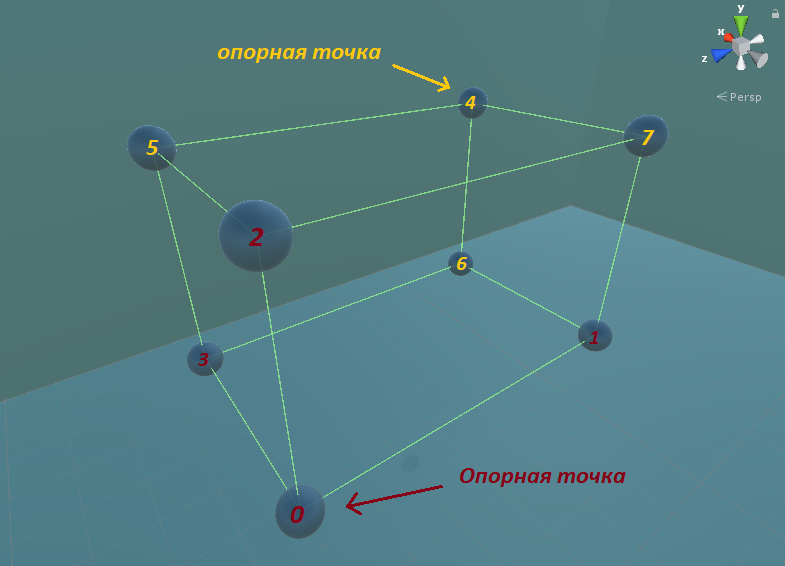
We can see how the points are formed
After finding the coordinates of the vertices, it is necessary to rotate each vector by the corresponding quaternion.
//...
for (int i = 0; i < 8; i++)
{
point[i] -= box.Center;//
point[i] = QuanRotation(point[i], box.Quaternion);//
point[i] += box.Center;//
}
//...
complete code for getting vertices
private static Vector3[] GetPoint(Box box)
{
Vector3[] point = new Vector3[8];
//
point[0] = box.Center - box.Size/2;
point[1] = point[0] + new Vector3(box.Size.x , 0, 0);
point[2] = point[0] + new Vector3(0, box.Size.y, 0);
point[3] = point[0] + new Vector3(0, 0, box.Size.z);
//
point[4] = box.Center + box.Size / 2;
point[5] = point[4] - new Vector3(box.Size.x, 0, 0);
point[6] = point[4] - new Vector3(0, box.Size.y, 0);
point[7] = point[4] - new Vector3(0, 0, box.Size.z);
//
for (int i = 0; i < 8; i++)
{
point[i] -= box.Center;//
point[i] = QuanRotation(point[i], box.Quaternion);//
point[i] += box.Center;//
}
return point;
}
Let's move on to projections.
Act 3. Search for dividing axes
The next step is to find the set of axes that claim to be dividing.
Recall that it can be found in the following sets:
- Plane normals of each cube (red)
- Vector product of the edges of the cubes where X is the edges of the first cube (green) and Y is the second (blue).

In order to obtain the necessary axes, it is enough to have four vertices of the cube, which form an orthogonal system of vectors. These vertices are in the first four cells of the point array that we formed in the second act.

It is necessary to find the plane normals generated by the vectors:
- and
- and
- and
To do this, it is necessary to iterate through the pairs of edges of the cube so that each new sample forms a plane orthogonal to all the previous obtained planes. It was incredibly difficult for me to explain how it works, so I have provided two versions of the code to help you understand.
this code allows you to get these vectors and find the normals to the planes for two cubes (an understandable option)
private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
//
Vector3 A;
Vector3 B;
//
List<Vector3> Axis = new List<Vector3>();
//
A = a[1] - a[0];
B = a[2] - a[0];
Axis.Add(Vector3.Cross(A,B).normalized);
A = a[2] - a[0];
B = a[3] - a[0];
Axis.Add(Vector3.Cross(A,B).normalized);
A = a[1] - a[0];
B = a[3] - a[0];
Axis.Add(Vector3.Cross(A,B).normalized);
//
A = b[1] - b[0];
B = b[2] - b[0];
Axis.Add(Vector3.Cross(A,B).normalized);
A = b[1] - b[0];
B = b[3] - b[0];
Axis.Add(Vector3.Cross(A,B).normalized);
A = b[2] - b[0];
B = b[3] - b[0];
Axis.Add(Vector3.Cross(A,B).normalized);
//...
}
But you can make it easier:
private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
//
Vector3 A;
Vector3 B;
//
List<Vector3> Axis = new List<Vector3>();
//
for (int i = 1; i < 4; i++)
{
A = a[i] - a[0];
B = a[(i+1)%3+1] - a[0];
Axis.Add(Vector3.Cross(A,B).normalized);
}
//
for (int i = 1; i < 4; i++)
{
A = b[i] - b[0];
B = b[(i+1)%3+1] - b[0];
Axis.Add(Vector3.Cross(A,B).normalized);
}
//...
}
We also have to find all the vector products of the edges of the cubes. This can be organized by a simple search:
private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
//...
//
//...
//
for (int i = 1; i < 4; i++)
{
A = a[i] - a[0];
for (int j = 1; j < 4; j++)
{
B = b[j] - b[0];
if (Vector3.Cross(A,B).magnitude != 0)
{
Axis.Add(Vector3.Cross(A,B).normalized);
}
}
}
return Axis;
}
Complete code
private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
//
Vector3 A;
Vector3 B;
//
List<Vector3> Axis = new List<Vector3>();
//
for (int i = 1; i < 4; i++)
{
A = a[i] - a[0];
B = a[(i+1)%3+1] - a[0];
Axis.Add(Vector3.Cross(A,B).normalized);
}
//
for (int i = 1; i < 4; i++)
{
A = b[i] - b[0];
B = b[(i+1)%3+1] - b[0];
Axis.Add(Vector3.Cross(A,B).normalized);
}
//
for (int i = 1; i < 4; i++)
{
A = a[i] - a[0];
for (int j = 1; j < 4; j++)
{
B = b[j] - b[0];
if (Vector3.Cross(A,B).magnitude != 0)
{
Axis.Add(Vector3.Cross(A,B).normalized);
}
}
}
return Axis;
}
Act 4. Projections on the axis
We have come to the most important point. Here we have to find the projections of the cubes on all potential dividing axes. The theorem has one important consequence: if objects intersect, then the axis on which the intersection of the projection of the cubes is minimal is the direction (normal) of the collision, and the length of the intersection segment is the penetration depth.
But first, recall the formula for the scalar projection of the vector v onto the unit vector a :
private static float ProjVector3(Vector3 v, Vector3 a)
{
a = a.normalized;
return Vector3.Dot(v, a) / a.magnitude;
}
Now we will describe a function that will determine the intersection of projections on the candidate axes.
The input is the vertices of two cubes, and a list of potential dividing axes:
private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
for (int j = 0; j < Axis.Count; j++)
{
//
//
}
// , ,
// .
}
The projection onto the axis is set by two points that have maximum and minimum values on the axis itself:
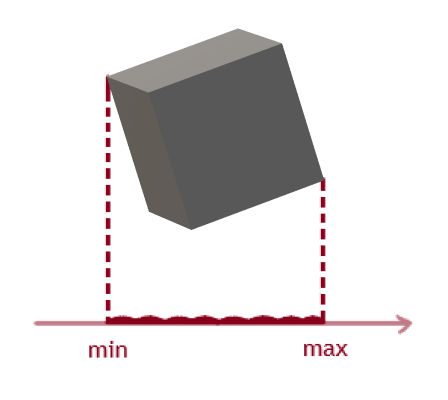
Next, we create a function that returns the projection points of each cube. It takes two return parameters, a vertex array and a potential dividing axis.
private static void ProjAxis(out float min, out float max, Vector3[] points, Vector3 Axis)
{
max = ProjVector3(points[0], Axis);
min = ProjVector3(points[0], Axis);
for (int i = 1; i < points.Length; i++)
{
float tmp = ProjVector3(points[i], Axis);
if (tmp > max)
{
max = tmp;
}
if (tmp < min)
{
min= tmp;
}
}
}
So, applying this function ( ProjAxis ), we get the projection points of each cube.
private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
for (int j = 0; j < Axis.Count; j++)
{
// a
float max_a;
float min_a;
ProjAxis(out min_a,out max_a,a,Axis[j]);
// b
float max_b;
float min_b;
ProjAxis(out min_b,out max_b,b,Axis[j]);
//...
}
//...
}
Next, based on the projection vertices, we determine the intersection of the projections:
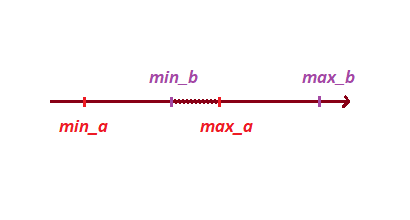
To do this, let's put our points into an array and sort it, this method will help us determine not only the intersection, but also the depth of the intersection.
float[] points = {min_a, max_a, min_b, max_b};
Array.Sort(points);
Note the following property:
1) If the segments do not intersect , then the sum of the segments will be less than the segment by the formed extreme points:

2) If the segments intersect , then the sum of the segments will be greater than the segment by the formed extreme points:
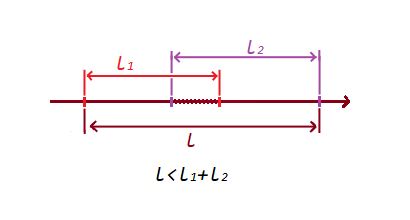
With such a simple condition, we checked the intersection and non-intersection segments.
If there is no intersection, then the depth of intersection will be zero:
//...
//
float sum = (max_b - min_b) + (max_a - min_a);
//
float len = Math.Abs(p[3] - p[0]);
if (sum <= len)
{
//
//
return Vector3.zero;
}
//,
//....
Thus, it is enough for us to have at least one vector on which the projections of the cubes do not intersect, then the cubes themselves do not intersect. Therefore, when we find the dividing axis, we can skip checking the remaining vectors and terminate the algorithm.
In the case of intersection of cubes, everything is a little more interesting: the projection of the cubes on all vectors will intersect, and we must determine the vector with the minimum intersection.
Let's create this vector before the loop, and we will store the vector with the minimum length in it. Thus, at the end of the cycle, we get the desired vector.
private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
Vector3 norm = new Vector3(10000,10000,10000);
for (int j = 0; j < Axis.Count; j++)
{
//...
}
// , ,
return norm;
{
And every time we find the axis on which the projections intersect, we check whether it is the smallest in length among all. we multiply such an axis by the length of the intersection, and the result will be the desired normal (direction) of intersection of the cubes.
I also added a definition of the orientation of the normal with respect to the first cube.
//...
if (sum <= len)
{
//
//
return new Vector3(0,0,0);
}
//,
// - 2 1
//(. )
float dl = Math.Abs(points[2] - points[1]);
if (dl < norm.magnitude)
{
norm = Axis[j] * dl;
//
if(points[0] != min_a)
norm = -norm;
}
//...
The whole code
private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
Vector3 norm = new Vector3(10000,10000,10000);
for (int j = 0; j < Axis.Count; j++)
{
// a
float max_a;
float min_a;
ProjAxis(out min_a,out max_a,a,Axis[j]);
// b
float max_b;
float min_b;
ProjAxis(out min_b,out max_b,b,Axis[j]);
float[] points = {min_a, max_a, min_b, max_b};
Array.Sort(points);
float sum = (max_b - min_b) + (max_a - min_a);
float len = Math.Abs(points[3] - points[0]);
if (sum <= len)
{
//
//
return new Vector3(0,0,0);
}
float dl = Math.Abs(points[2] - points[1]);
if (dl < norm.magnitude)
{
norm = Axis[j] * dl;
//
if(points[0] != min_a)
norm = -norm;
}
}
return norm;
}
Conclusion
The project with implementation and example is uploaded to GitHub, and you can view it here .
My goal was to share my experience in solving problems related to determining the intersections of two convex objects. And it is also accessible and understandable to tell about this theorem.