
Many thanks. I apologize for sitting here. I am a very old man.
My topic today is in a sense very special, because it is very ancient. Kinks are an integral part of human life, they are always there. The ancients wrote about this. This thing is largely out of our control. And in a sense, they seem to be an extreme degree of complication - just a complete mess.
There are many types of disorder. So, by pure coincidence, many years ago I began to deal with this form of complication, and, to my complete surprise, I found signs, and, I must say, very clear signs of order in the kinks. So today I would like to present to you some examples of what this means. I prefer the word “broken” to “uneven” because for someone who studied Latin, like me in my distant youth, unevenness is the opposite of evenness. But this is not the case.
Equality is the opposite of fracture, because the world for the most part appears to us as full of fractures.
Let me show you a couple of objects. Some of them are artificially created. Others are very real, in a certain sense. This is the real thing.

This is cauliflower. Why am I showing you cauliflower, an ordinary and ancient plant? Because, in spite of its routine and antiquity, it is complex and simple. it is complex and simple. For example, it is not difficult to weigh it. Weight matters if we're going to eat it. But suppose we are going to measure its surface. This is getting interesting. Having cut out one of the cauliflower flowers with a sharp knife, and looking closely, we see the whole cauliflower, only of a smaller size. Then you can cut again and again and again and again and again ... And you get smaller and smaller specimens of cauliflower. Human experience has shown that there are forms with such an interesting property that each part is similar to the whole, but of a smaller size. And what did the person learn from this fact? Very little.
In connection with the study of this problem, I discovered something completely amazing: kink can be measured by a number, say, 2.3 or 1.2, and sometimes much more. One day, a friend of mine brought a photograph and, half in jest, asked: "What is the kink of this curve?" I said, “Slightly less than one and a half.” As it turned out, it was equal to 1.48. It didn't take me long as I studied these things for so long. The numbers in question indicate the degree of fracture of the surface.

Let me make a reservation right away that the surfaces are absolutely artificial and were created on a computer. The only starting point was the number. This number is kink. The fracture on the left is the result of copying from several landscapes. On the right - I set a higher kink myself. If you look closely, after a while you can recognize the differences in these two cases with the naked eye.
Man had to get used to the concept of fracture. This is very broken, but this, one might say, is smooth, but this is completely smooth. Few things are very smooth. Let us now ask ourselves the question: what is the surface of the cauliflower? It can be measured and measured and measured ... The more accurate the measurement, the larger the surface, and so on, down to very small distances. What is the length of the coastline of these lakes? The more accurate the measurement, the longer it will turn out. The concept of coastline length, which seems so obvious because it is often quoted, is in fact completely wrong: there is simply no such thing. There must be a different approach.
And what is the use of this knowledge? Surprisingly, there are many benefits. To begin with, the artificial landscapes that I, shall we say, have invented are constantly used in cinematography. We see mountains in the distance. It may be mountains, but it may well be just flowing formulas. This is very easy to achieve. It used to take a long time, but now it is a mere trifle. Take a look here. This is real light.
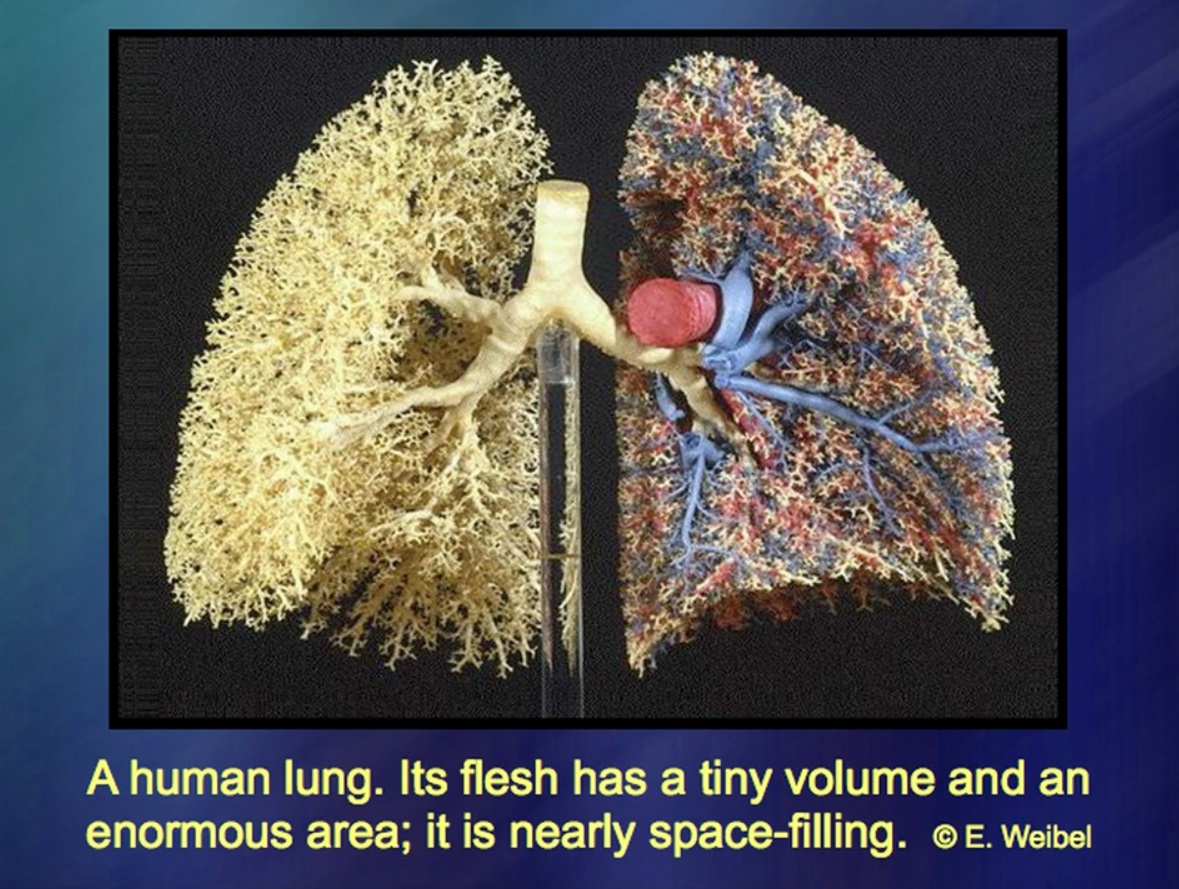
The lung is a very strange object. We all know very well that it has some weight. It is also known that the volume of the lung is very small. What about lung area? Anatomists have long debated this issue. It is believed that in a normal man, the area of the lung is equal to the area of one basketball. Others argue that there are no five such balls. The discrepancies are colossal. Why? Because the area of the lung is a very vaguely defined concept. The bronchi branch and branch deeper and deeper. And they stop branching not because of some principle, but because of purely physical conditions, because of mucus inside the lung. This is how a much larger lung is formed: the bronchi branch out deeper and deeper, while the gap between them is approximately the same for a whale, and for a person, and for a small rodent.
So what is the use of this? Surprisingly and even astonishingly, anatomists had a poor idea of the structure of the lung until recently. I think my mathematical research, surprisingly enough, was of great help to surgeons who study lung diseases, as well as liver diseases, where there are such branch systems with a lack of intelligible geometry. In other words, I had to create geometry for something that does not have its own geometry. A surprising quality was found: very often the rules of this geometry are extremely short. You start with short formulas, apply them several times, sometimes repeatedly, over and over again. The same repeat. And in the end it turns out something like that.
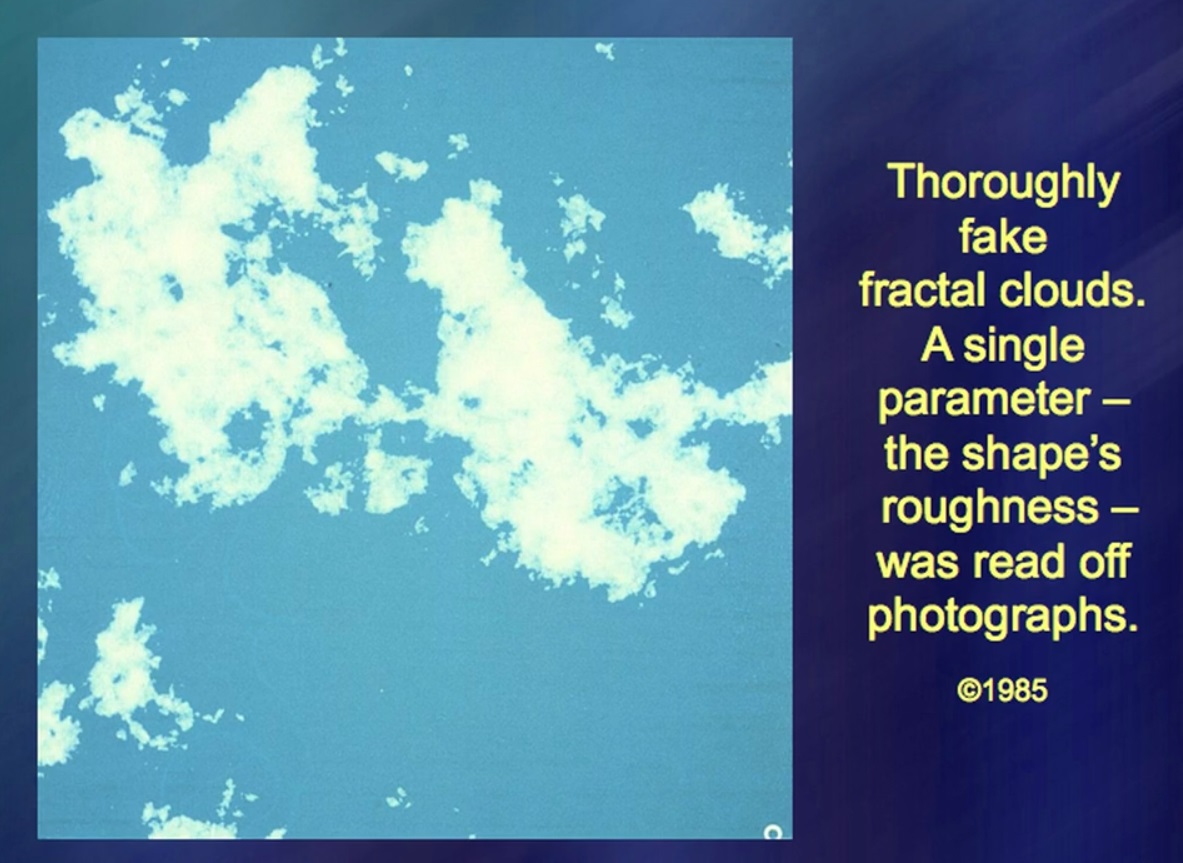
This cloud is completely artificial, 100%. Okay, 99.9%. The only natural element here is number, the fracture of the cloud - this number is taken from nature. Such a complex thing as a cloud, so unstable, changeable, obeys a simple rule. This simple rule is not an explanation for cloudiness. But the sea of clouds must take this rule into account. I don't know how perfect these old photos are. I did this intensively, but then my attention was directed to other phenomena.
And here is one more interesting thing. One of the revolutionary events in the history of mathematics, insufficiently appreciated by many, took place about 130 years ago, 145 years ago. Mathematicians began to create non-existent forms. Among mathematicians, the ability of a person to create something that never existed in nature has come to be appreciated, and to an absolutely unimaginable degree. In particular, they were able to invent a curve that fills the entire plane to the last point. A curve is a curve, a plane is a plane, and the two do not fit together. It turned out that they do fit together.
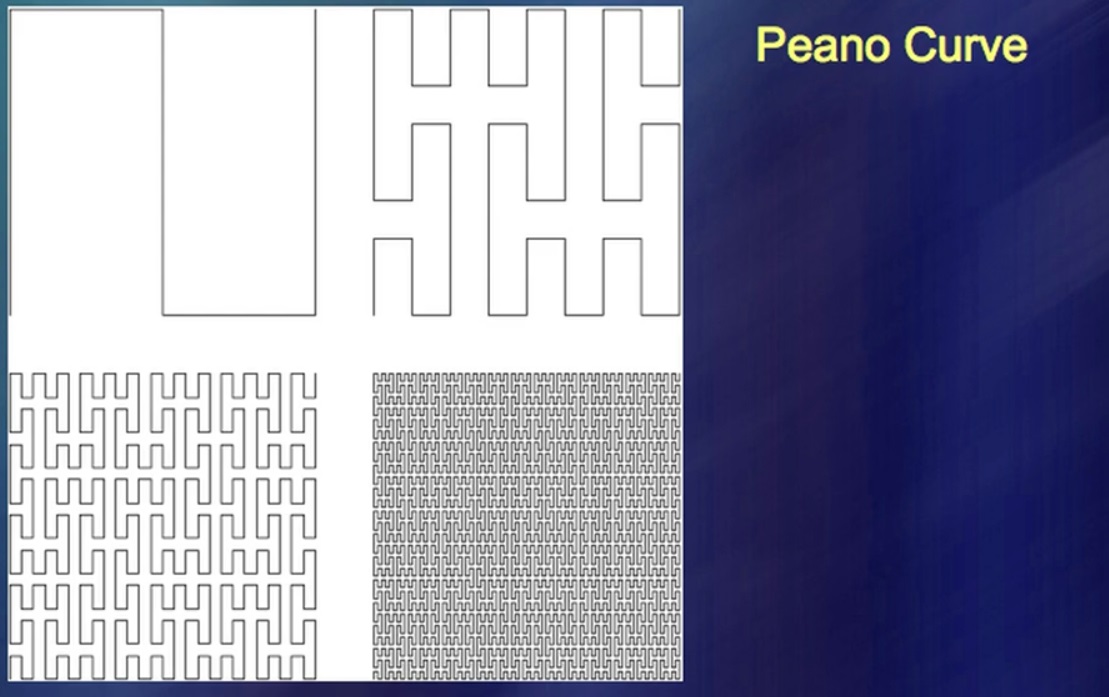
A man named Peano identified such curves, and they generated exceptional interest. They are very important and arousing interest in large part because there has been some sort of division of mathematics into one that is based on reality and one that comes from pure reason. Unfortunately, I happened to prove that what became known through the efforts of the pure reason, in fact, has long been known in a different form. Here I have a system of rivulets in the form of curves filling the plane.

In itself, this is history. It was between 1875 and 1925, an amazing time when mathematics was preparing to break away from the real world. Certain objects have served as an illustration of the gap, since my childhood and my student years, the gap between mathematics and visible reality. However, I managed to rethink them, turn them upside down, and with their help describe some aspects of the complexity of nature.
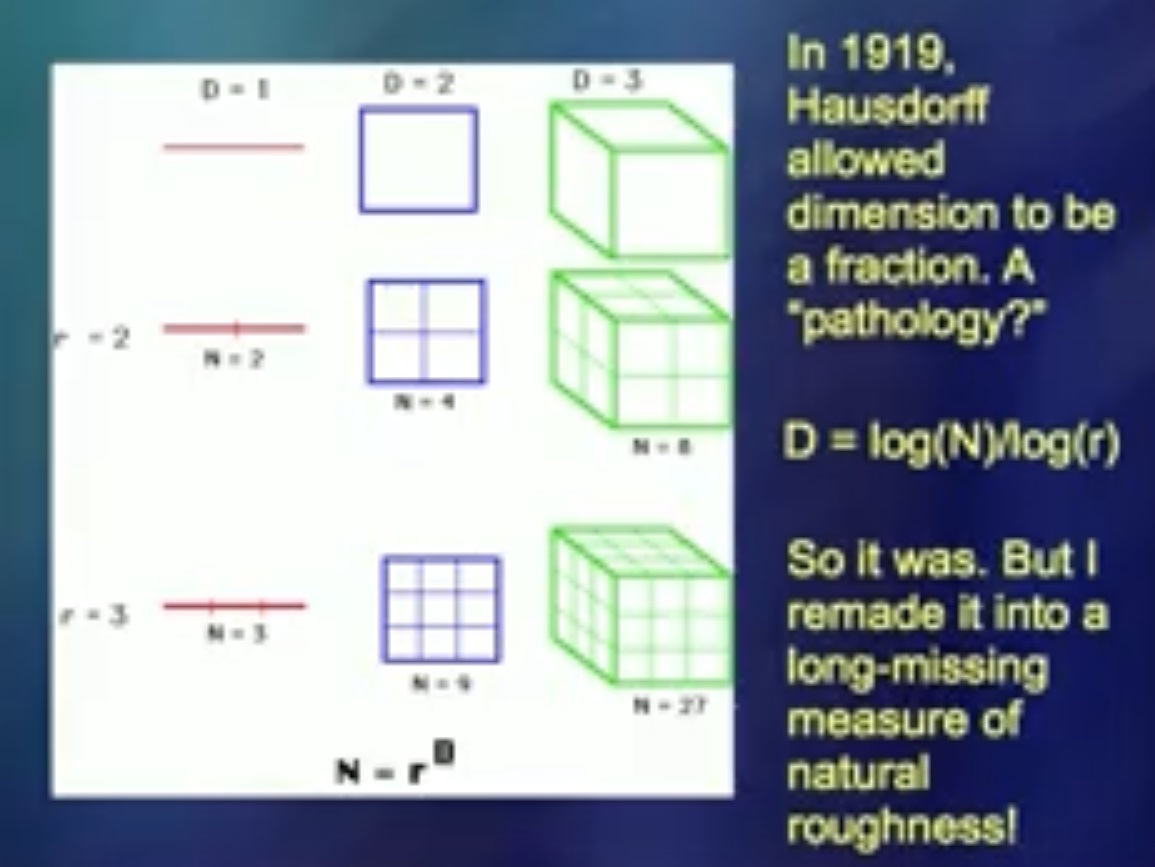
In 1919, a man named Hausdorff identified a number that could be considered a mathematical joke. But I have found that this number is a good tool for measuring kink. When I first told my colleagues about this, they said, “Don't be silly. This is something ... ”Actually, I was not doing stupid things.

The great artist Hokusai knew this very well. At the bottom of the picture are algae. Hokusai did not know the necessary mathematics: it simply did not exist then. Moreover, being Japanese, he [at the time] had no contact with the West. But art has long contained fractal elements. I can talk about this for a long time.

The Eiffel Tower has fractal elements. I read Eiffel's book about his tower - the scope of his understanding is amazing.
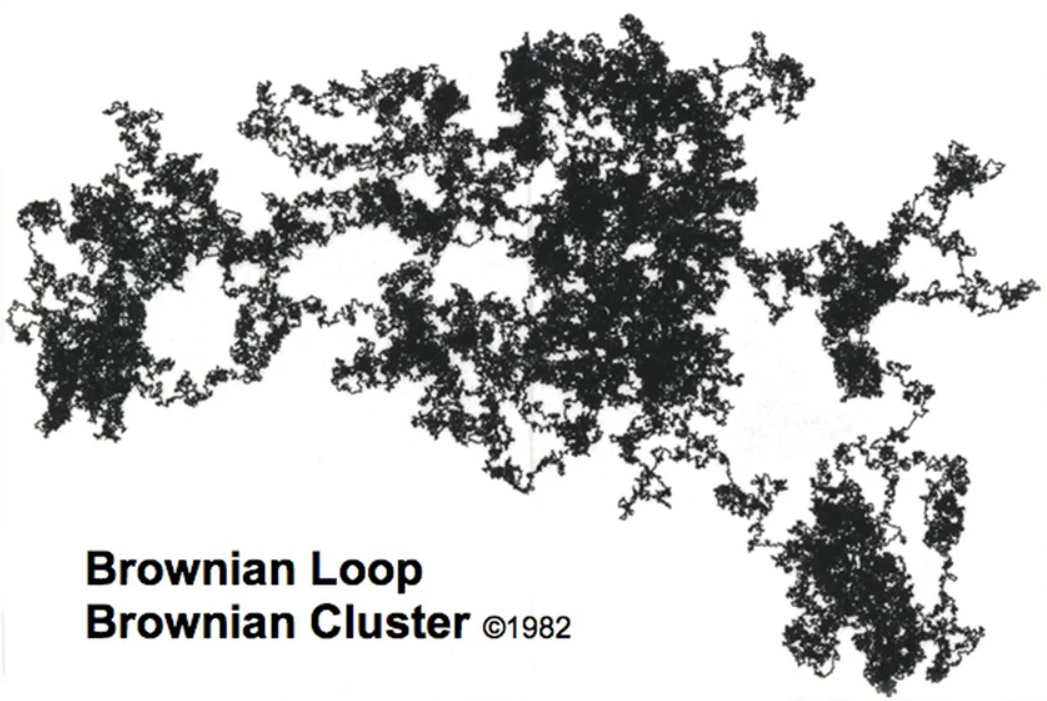
Here is a mess within a mess. Brownian loop. Once I decided that I had gone through a considerable part of my professional life, and so many different things occupied me that I decided that it was time to test myself. Can I explore an object that everyone has been exploring for a long time and find something radically new in it? I began to study everything that falls into the category of Brownian motion. I tried different angles, tried different methods, and returned to where I started. Then I suggested to my assistant: “I don't see anything here. Can you paint over? " He did so, that is, he filled all the insides. "I managed…"

But I shouted: “Stop! Stop! Stop! Understood: this is an island. " Amazing. Brownian motion has a kink equal to two. I measure it, it turns out 1.33. I measure again and again. Long measurements, large Brownian movements. Again: 1.33. A mathematical problem immediately arises: how to prove it? It took my friends 20 years. Three had incomplete evidence. They joined forces and together they managed to get proof. As a result, they were awarded the famous [Fields] medal for mathematicians. Overall, mathematicians received three [Fields] medals for proving facts that I saw but could not prove.
Now people ask me everywhere: “How did it all start? How did your studies lead you to such unusual things? "
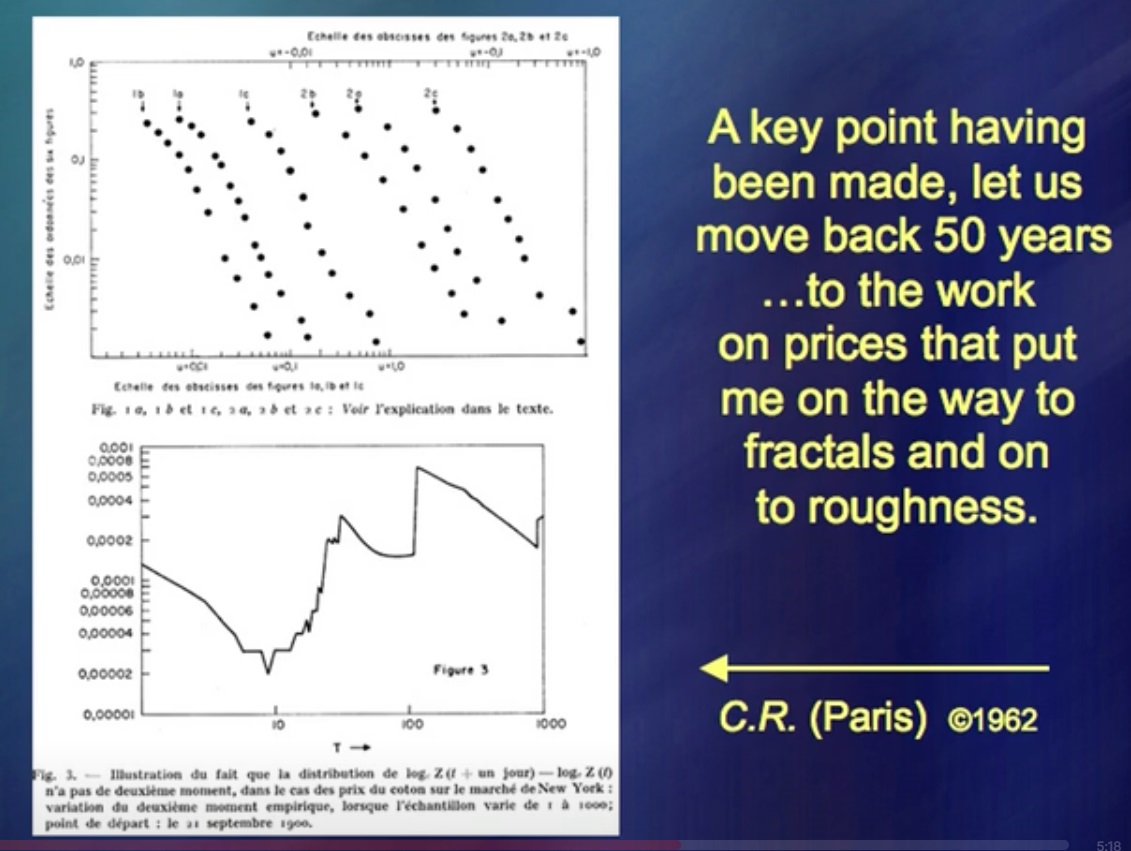
What allowed me to be simultaneously a mechanical engineer, geographer, mathematician, etc.? Oddly enough, but I started by studying the prices on the stock market.

I had a theory and I wrote books about it.
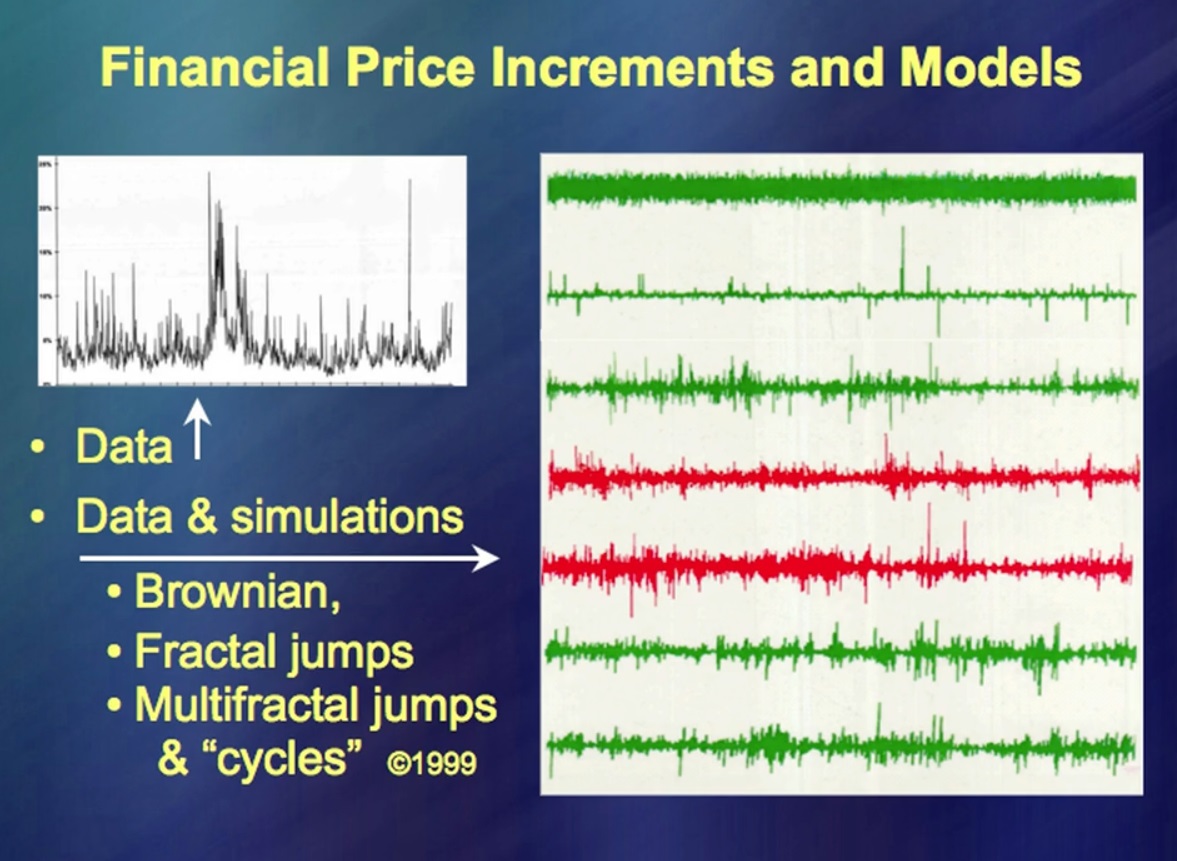
"Price movements of financial instruments" On the left you can see the data for a long period, on the right, at the top - the data according to a very, very fashionable theory. It's extremely simple and you can write a lot of books about it very quickly. (Laughter) There are thousands of books on this topic. Now compare with real price movements. And where are they? Additional lines include real price movements as well as a small fake on my part. The main idea there was that you need to be able to do ... What is it called? … Simulation of price fluctuations. This worked great 50 years ago.
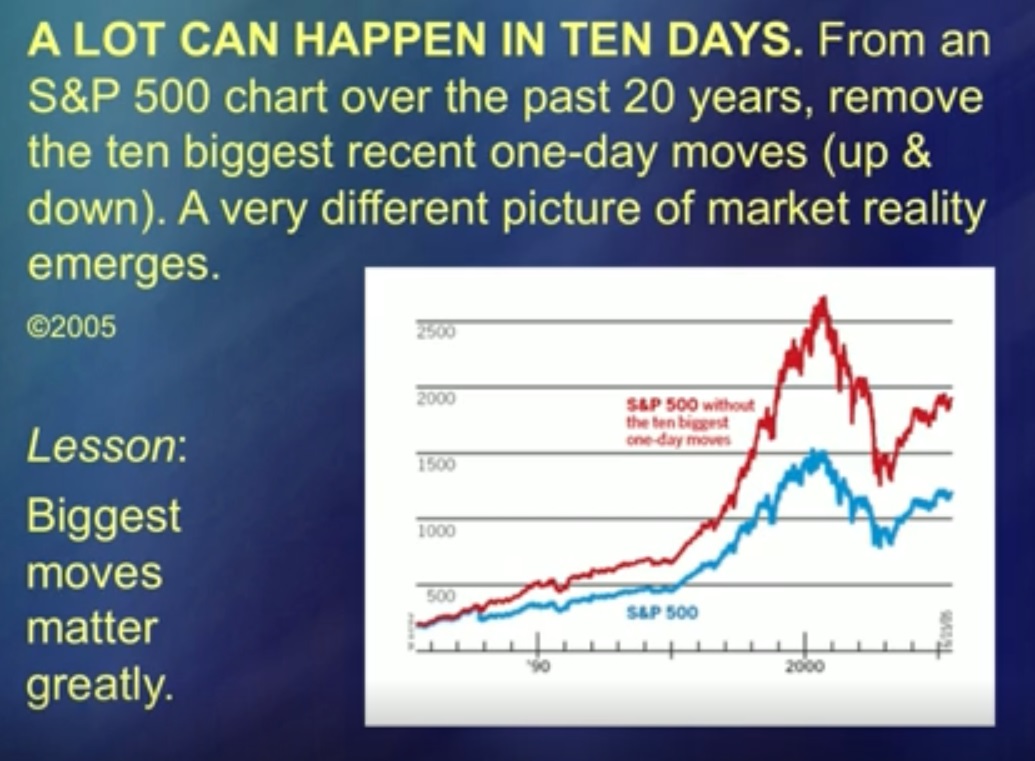
For 50 years, my idea was ridiculed because it could have been done easier. But now, I tell you, they began to listen to me. (Laughter) These two curves represent averages. Blue is the Standard and Poor's [S&P 500] and red is the Standard and Poor's, from which the 5 largest price spikes have been subtracted. The leap certainly spoils the analysis, and in many studies it is considered [non-analytic] a special case. “Incredible coincidence, intervention of the Lord. Well, a little thing, you can just put it aside. " The interventions of the Lord on this graph, and there are exactly five of them, as it turns out, are as important as everything else. In other words, the Lord's interventions cannot be put aside.
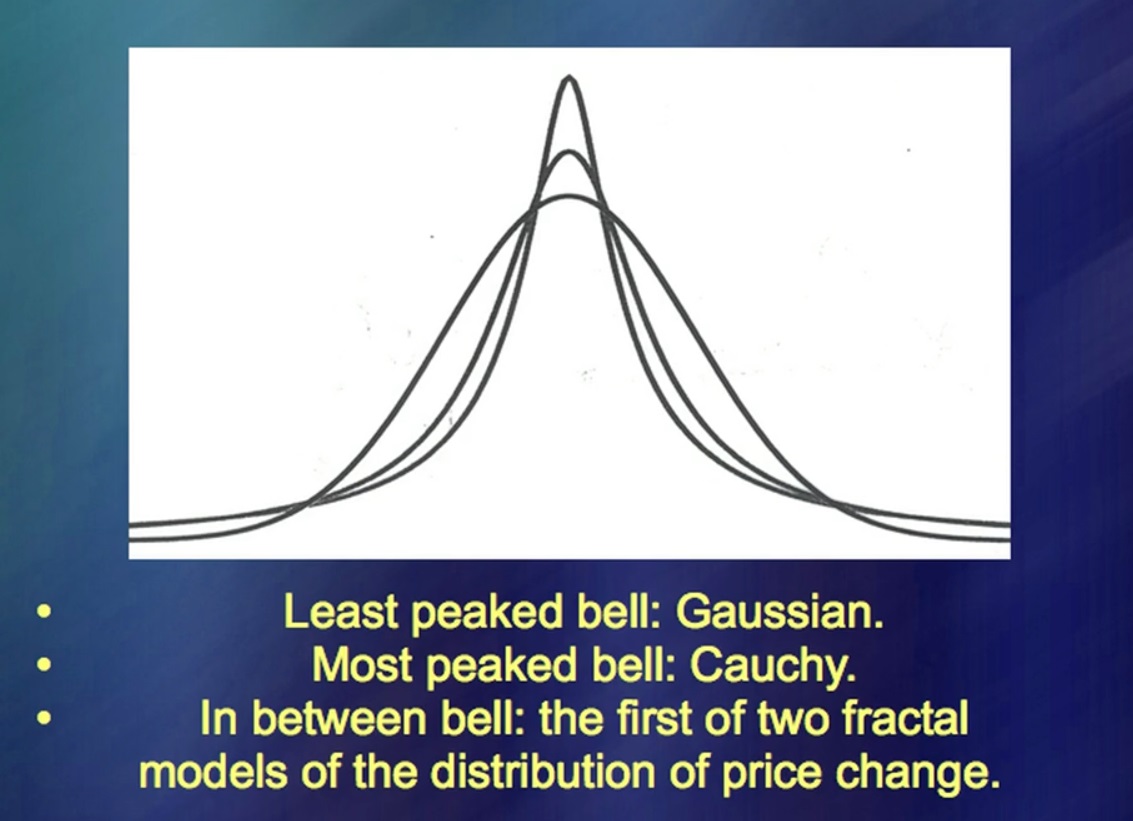
It is a being, it is the very object of analysis. If you deal with them, you can also deal with price movements. But I haven't figured out the jumps, then you can analyze the so-called noise as much as you like, but this analysis will not make sense. These curves show the impact.

Now I will turn to the last topic - the set named after me. In a way, this is the story of my life. My adolescence was spent in France, which was occupied by Germany in those years. Since I thought that at any moment I might not be, I had big dreams. After the war, I met my uncle again. My uncle was an outstanding mathematician and he said: “Here's a problem for you. 25 years ago I could not solve it, and no one can solve it. This is the construction of one mathematician named Gaston Julia and another named Pierre Fatou. If you can find something new here - anything - consider that your career is secured. " Very simple. I began to study this problem, and, like thousands of those who tried to do it before me, achieved nothing.
But then computers came along. And I decided that I needed to apply computing power not to new mathematical problems - like, for example, this curving thing: this is a new problem - but to old problems. And I switched from the so-called real numbers, i.e. from points on a straight line to complex numbers, and these are points on a plane, that is, what is required in this problem. The result is such a figure.

This one is of exceptional complexity. The equation is hidden in it: z transforms into z ^ 2 + c. So simple and boring, so uninteresting. Now let's run it once, twice ... Twice is enough. About a miracle! This is what appears. I'm not going to explain these things here, but it turns out this is what and this is what.


Figures of such complexity, such harmony and such beauty are obtained repeatedly, over and over and over again. My main discovery was that these islands have the same shape, more or less, as the whole figure. The result is such stunning baroque jewelry.

And all of this short formula, in which there is everything - how much is there? - five icons. And this is the result.

The color was added for two reasons. Firstly, because the figures are so complex that it is difficult to see what meaning the numbers carry. And you need to choose some kind of system to reflect them on the plane. Therefore, I took it as a principle to always represent the figures in different colors: one color means one thing, and another means another, etc. It's so hard.
In 1990, I was in the UK, in Cambridge, where I was awarded a prize from the university. Three days later, one pilot, flying over the field, saw this.

Where would such a thing come from? Of course - from the aliens.
One of the newspapers in Cambridge published an article about this "discovery", and the next day received 5,000 letters, which said that this is the Mandelbrot set, just very large.

Let me finish. This picture is obtained through pure mathematics. Simple rules can create a bottomless miracle if repeated endlessly.
Translated by Namik Kasumov
Reviewed by Ekaterina Tsvetkova

Learn the details of how to get a sought-after profession from scratch or Level Up in skills and salary by completing SkillFactory paid online courses:
- Machine Learning (12 )
- Data Science (12 )
- (9 )
- «Python -» (9 )
- Data Sciene 2020
- Data Science . Business Science
- Data Scientist
- Data Scientist -
- Data Science
- Data Science : «data»
- Data Sciene : Decision Intelligence