I remember seeing the photo above on Flickr one day and breaking my brain trying to figure out what was wrong with it. The point was that the propeller was rotating at the time when the motion sensor in the camera was "reading readings", that is, during the exposure of the camera, there was some movement. This is really worth thinking about, let's think about it together.
Many digital cameras today use a CMOS sensor as their "sensing" device, also known as an active pixel sensor., which works by accumulating electronic charge when light strikes it. After a certain time - exposure time - the charge is transferred line by line back to the camera for further processing. The camera then scans the image, keeping the rows of pixels line by line. The image will be distorted if there is any movement during the shooting. For illustration, imagine shooting a rotating propeller. In the animations below, the red line corresponds to the current read position and the propeller continues to rotate as it reads. The part under the red line is the resulting image.
The first propeller makes 1/10 of a revolution during exposure:
Subscribe to the channels:
@Ontol - the most interesting texts / videos of all times and peoples, influencing the picture of the world
@META LEARNING - where I share my most useful findings about education and the role of IT / games in education (as well as Anton's thoughts on this topic Makarenko, Seymour Papert, Paul Graham, Joseph Licklider, Alan Kay)
The image is slightly distorted, but nothing critical. The propeller will now move 10 times faster, making a full rotation during the exposure:
This already looks like the picture that we saw at the beginning. Five times per exposure:
This is already a little too much, so you can go off the reels. Let's have some fun and check how different objects will look at different rotation speeds per exposure.
Exactly the same propeller:
Large propeller blades:
Car wheel:
We can perceive the rolling shutter effect as some kind of transformation of the coordinates of a real object from "object space" to the "image space" of a distorted object. The animation below shows what happens to the Cartesian coordinate system as the number of revolutions increases. At low speeds, the deformation is insignificant - the number increases to one, and each side of the coordinate system moves sequentially to the right side of the image. This is a rather complex transformation to grasp, but easy to understand.
Let the image be I (r, θ), the real (rotating) object will be f (r, θ), where (r, θ) are 2D polar coordinates. We chose polar coordinates for this task due to the rotational motion of the objects.
The object rotates with an angular frequency ω, and the shutter moves along the image with a speed v vertically. At position (r, θ) in the picture, the distance that the shutter has traveled since the beginning of the exposure is y = rsinθ, where the time elapsed since that moment is (rsinθ) / v. During this time, the object rotated by (ω / v) rsinθ) radians. So, we get
I (r, θ) = f (r, θ + (ω / v) rsinθ),
which is the required transformation. The ω / v ratio is proportional to the number of rotations per exposure and parameterizes the transformation.
To get a deeper understanding of the obvious propeller shapes, we can consider an object consisting of P propellers, where f is nonzero only for
θ = 2π / P, 4π / P… 2π = 2pπ / P for 1 <p <P.
Image I is non-zero for θ + (ω / v) rsinθ = 2pπ / P or
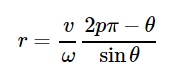
In the Cartesian coordinate system it becomes
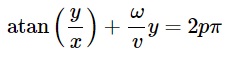
and helps us in explaining the reason why the propellers take an S-shape - it is simply a function of the arctangent in image space. Cool. Below I plotted this function with a set of five propeller blades with slightly different initial offsets, you can see this in the playback. They are very similar to the shapes in the animations above.
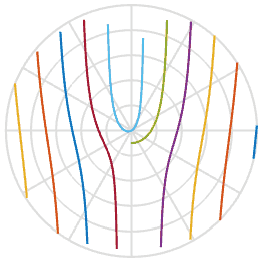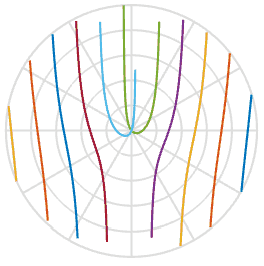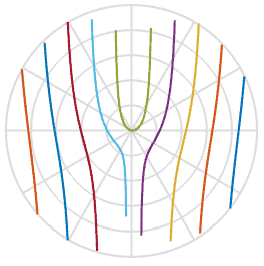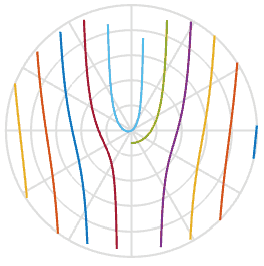
Since we learned a little more about the process, can we fix the damaged photos? Using one of the images above, I can draw a line through it, rotate back and insert those pixels into the new image. In the animation below, I scan the image on the left, marked with a red line, and then rotate the pixels along that line to get a new image. This way we can recreate the image of a real object, even if suddenly an annoying rolling shutter spoiled your photo.
Eh, if I was better at Photoshop, I would extract the propellers from the original photo on Flickr, edit it and put it back into the photo. I think I know what I'll do in the future.
If you want to know the actual number of blades in the photo at the beginning of the post and the speed of rotation, you can read this excellent post on Tumblr by Daniel Walsh , in which he gives a mathematical explanation.
He thinks we can count the number of blades by subtracting the "bottom" blades from the "top" ones, so we get three blades in that picture. We also know that the propeller spins about twice during the exposure, so if we try to "undo" the rotation at several different speeds, we get something like this:
I had to figure out where the center of the propeller was, so I drew a circle. Apparently, the center should be somewhere nearby. Unfortunately, one blade is missing, but there is enough information to display it.
I found the place where everything intersects the most, so at this rotational speed (2.39 revolutions per exposure), this is what the original image and blades look like:
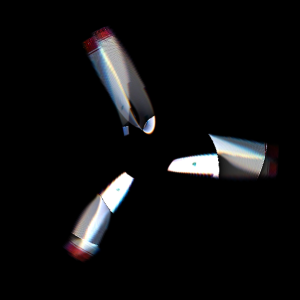
Unfortunately, the picture is not perfect, but at least it is very close to reality.
About the author: Jason Cole is a graduate student from London who is passionate about math, physics and data visualization. Here's his website . And the article was published here .
Hacker News Discussion
add. video
Subscribe to the channels:
@Ontol - the most interesting texts / videos of all times and peoples, influencing the picture of the world
@META TRAINING , where I share my most useful findings about education and the role of IT / games in education (as well as Anton's thoughts on this topic Makarenko, Seymour Papert, Paul Graham, Joseph Licklider, Alan Kay)
Learn the details of how to get a sought-after profession from scratch or Level Up in skills and salary by completing SkillFactory paid online courses:
- Machine Learning Course (12 weeks)
- Learning Data Science from scratch (12 months)
- Analytics profession with any starting level (9 months)
- Python for Web Development Course (9 months)