Heap Bottom Sort

This is the final article in a series about heap sorting. In previous lectures, we looked at a wide variety of heap structures showing excellent speed results. The question arises: what kind of heap is most effective when it comes to sorting? The answer is: the one that we will look at today.

EDISON .




— « » — -, CRM-, , iOS Android.



;-)

The fancy heaps we looked at earlier are fine, but the most efficient heap is the standard heap with improved clearing.



What a clearing is, why is it needed in a heap and how it works is described in the very first part of a series of articles.



The standard sifting in classical heap sorting works roughly "head-on" - an element from the root of a subtree is sent to the clipboard, elements from a branch are moved up according to the results of comparison. Everything is quite simple, but it turns out too many comparisons.







In the ascending lane, comparisons are saved due to the fact that parents are hardly compared with their descendants, basically, only descendants are compared with each other. In an ordinary heapsort, both the parent is compared with the children and the children are compared with each other - therefore, there are almost one and a half times more comparisons with the same number of exchanges.



So how it works, let's take a look at a specific example. Let's say we have an array in which a heap is almost formed - all that remains is to sift through the root. For all other nodes, the condition is fulfilled - any descendant is no more than its parent.



First of all, from the node for which sifting is performed, you need to go down, along large descendants. A bunch of binary - that is, we have a left descendant and a right descendant. We get down to that branch where the descendant is larger. At this stage, the main number of comparisons takes place - the left / right descendants are compared with each other.







Having reached the sheet at the last level, we thereby decided on the branch in which the values ​​need to be shifted up. But you do not need to move the entire branch, but only the part that is larger than the root from which you started.



Therefore, we go up the branch up to the nearest node, which is greater than the root.







The last step - using the buffer variable, we shift the values ​​of the nodes up the branch.







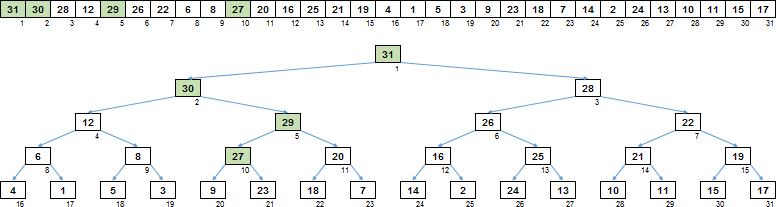
That's it. The ascending sifter formed a sorting tree from the array, in which any parent is larger than its descendants.



Final animation:

Python 3.7 implementation

The basic sorting algorithm is no different from regular heapsort:

#    
def HeapSortBottomUp(data):

    #    
    #   -   
    # (   )       
    for start in range((len(data) - 2) // 2, -1, -1):
        HeapSortBottomUp_Sift(data, start, len(data) - 1) 

    #        
    #        .
    for end in range(len(data) - 1, 0, -1): 
        #       
        #    
        data[end], data[0] = data[0], data[end]
        #        
        #   
        #     
        HeapSortBottomUp_Sift(data, 0, end - 1)
    return data

Descent to the bottom sheet can be conveniently / visually taken out in a separate function:

#      
#   
def HeapSortBottomUp_LeafSearch(data, start, end):
    
    current = start
    
    #  ,  
    #  (  ) 
    while True:
        child = current * 2 + 1 #  
        #  ,    
        if child + 1 > end: 
            break 
        #  ,   
        if data[child + 1] > data[child]:
            current = child + 1
        else:
            current = child
    
    #  ,    
    child = current * 2 + 1 #  
    if child <= end:
        current = child
        
    return current

And most importantly - a clearing, first going down, then emerging upward:

#  
def HeapSortBottomUp_Sift(data, start, end):
    
    #        
    current = HeapSortBottomUp_LeafSearch(data, start, end)
    
    #  ,    
    #     
    while data[start] > data[current]:
        current = (current - 1) // 2
    
    #   ,
    #      
    temp = data[current]
    data[current] = data[start]
    
    #        
    # -     
    while current > start:
        current = (current - 1) // 2
        temp, data[current] = data[current], temp  

Purely empirically - according to my measurements, upward sorting by a heap works 1.5 times faster than regular sorting by a heap.



According to some information (on the page of the algorithm in Wikipedia, in the PDF cited in the "Links" section), BottomUp HeapSort is on average ahead of even quick sort - for fairly large arrays of 16 thousand elements or more.

References

Bottom-up heapsort



A Variant of Heapsort with Almost Optimal Number of Comparisons



Building Heaps Fast



A new variant of heapsort beating, on an average, quicksort (if n is not very small)

Series articles:

• Excel application AlgoLab.xlsm
• Sorting exchanges
• Insertion Sorts
• Sort by selection
  • Heap sorts: n-ary pyramids
  • Heap Sorts: Leonardo Numbers
  • Heap Sorts: Weak Heap
  • Bunch Sorts: Cartesian Tree
  • Heap Sorts: Tournament Tree
  • Heap Sort: Rising Sifter
• Merge Sorts
• Sort By Distribution
• Hybrid sorts

Today's sorting has been added to the AlgoLab application, who uses it - update the excel file with macros.