
Born to crawl - cannot fly. This phrase can be used both in a metaphorical sense and in a literal sense, because creatures without wings (or similarly functional body parts) are really not able to conquer the heavens. At least most of them. The rule would not be the rule if there were no exceptions. In the aspect of wingless flights, there are also exceptions - decorated tree snakes ( Chrysopelea). Representatives of this genus of snakes are capable of soaring - an extremely useful skill given that they live in the crowns of trees high above the ground. Scientists from the Polytechnic University of Virginia (USA) decided to consider the flight of a snake in terms of kinematics. What anatomical features allow snakes to fly (fall in a controlled manner, to be exact), what happens during flight in terms of kinematics, and how can this research help in robotics? The answers to these questions await us in the report of scientists. Go.
Basis of research
Decorated tree snakes are a genus of serpentine snakes found in South and Southeast Asia. Representatives of this genus cannot boast of large dimensions (body length only from 0.6 to 1.5 m) and deadly poison. Although the prey they hunt in the daytime would disagree with the latter. Given the habitat (tree crowns), these snakes have very few enemies, therefore they do not have a special need for strong poison. In addition, they have a much more effective tactic - they know how to plan.

Flying snakes, as they are popularly called, crawl through trees using tough scales along their belly, allowing them to move vertically. If the snake wants to move from one tree to another, it first creeps to the edge of the branch, then folds the body into the shape of the Latin letter “J” to aim (to determine the desired angle of “takeoff” and the landing site). Saying "let's go", the snake pushes its body forward and upward, drawing in its stomach and protruding its ribs (so its body becomes flatter and slightly concave). During gliding, the snake constantly makes serpentine body movements from side to side, which allows it to control the flight and land softly.
Side view of a long gliding flying snake Chrysopelea paradisi.
An additional advantage of such an unusual method of movement for snakes is an impressive energy saving, because the flight is much faster (and safer) than slowly crawling from tree to tree on the ground. From this short description alone, it is clear that there are many important elements in the mechanics of the flight of a kite; takeoff angle, body shape during takeoff and flight, body movement in flight, etc.
The most striking, especially for observers, aspect of the flight of the snake is the wavy movement of the body. This technique is used by many creatures on the planet to move on earth and on water. You don't have to go far, because the snakes themselves use it perfectly. Scientists note that the undulating movement on land and water has been studied quite well, but such pirouettes in the air are still a mystery.
In Chrysopelea snakes, waviness is characterized by an S-shaped body shape, a low waviness frequency (1–2 Hz), and a flattened aerodynamic cross-section of the body.

Image No. 1
In fact, the air waviness continuously rearranges the snake's body, transforming it into a wing in shape ( 1e). Previous research has shown that flying kites always perform wavy movements in flight. However, it remains unclear whether waviness is an essential part of a successful flight or is it just a habit. the behavioral aspect of moving on land, migrated to flight without any intentions.
If we take into account waviness on land and water, then we can assume that it generates thrust in the air. On solid media, undulating motion occurs due to the distributed contact forces over the ventral and lateral regions of the body, and in water, the displacement or absorption of fluid along the body causes forward movement. In both cases, the pure driving force acts primarily in the plane of undulation. Out-of-plane (vertical) body modulation can be used for secondary purposes such as decreasing resistance or increasing normal strength.
But for flying kites, successful planning requires the generation of aerodynamic forces necessary to compensate for the animal's weight. The forces of lift and resistance are created by the air flowing through the flattened body when it is accelerated downward by gravity, and the reciprocating motion caused by muscle contractions probably does not increase force generation.
Front view of the take-off and flattening of a flying snake Chrysopelea paradisi.
The resulting aerodynamic forces must act outside the plane of the waviness, and the waviness itself must constantly change the distribution of forces on the snake's body. It is also worth considering that flying kites can "flutter" not only horizontally, but vertically. This means that the kite flight model contains both pitch * and roll * elements .
Pitch * - angular movement relative to the horizontal transverse axis of inertia.In this study, scientists decided to examine in detail the role of undulation in snake flight. Using high-speed snake flight recordings, scientists were able to quantify airborne waviness. The data obtained allowed us to create an accurate three-dimensional model of snake flight.
Roll * - angular movement about its longitudinal axis.
Research results
Air undulation consists of a bundle of waves of horizontal and vertical bending. 11-17 markers were placed along the body of snakes (7 individuals) participating in the shooting of the flight (high take-off area of 8.3 m). Assessing the position changes of these markers allows you to accurately determine the structure of the undulation during flight.
Top view on the test planning of a flying snake Chrysopelea paradisi.
Infrared markers obtained during the planning of the Chrysopelea paradisi flying kite.
After 36 practical observations, the scientists created a 3D model of the snake's body ( r ).
Development of a 3D model of a flying snake Chrysopelea paradisi based on motion capture data.
Using the tangent vector (t̂ = ∂r / ∂s), it was possible to decompose the waviness into two angular bending waves that move along the body.
Horizontal and vertical waves are given by the following formulas:
θ̅ (s, t) = -tan -1 t̂ x / t̂ y
and
ψ̅ (s, t) = sin -1 t̂ z
where θ̅ (s, t) and ψ̅ (s, t ) Are the local angles that the body forms relative to the horizontal and vertical directions, as a function of the arc length s and time t.
The data shows that flying kites use two waves: a horizontal wave with a large amplitude and a vertical wave with a lower amplitude, both of which travel sequentially down the body from head to tail (image # 2).

Image No. 2
These waves form after the initial transient, when the snake jumps in a relatively straight pose and then forms a characteristic S-shaped pose for planning.
There are four features of air waviness that associate a vertical wave with a horizontal one ( 2a ). First, the vertical wave has spatial and temporal frequencies twice that of the horizontal wave. This indicates that the body has two times more vertical bends than the lateral bends ( 2a ,2f ). Second, the U-bends on the body of a flying kite can be identified as zero crossings on the bend angle plot ( 2b ). Third, these intersections are the maxima of the vertical wave, indicating that the horizontal and vertical waves are 90 ° out of phase. Fourth, maximum bending off-plane occurs at the U-bends and approximately in the middle of the straight segments. At U-bends, the cross-section of the "wing" of the snake folds due to the movement of the body outside the plane ( 1c , 1d ).
The shape of the traveling waves changes over time, as the snake accelerates and produces aerodynamic forces, however, some features still remain common. The horizontal wave is a flat-topped sinusoid whose amplitude (80-120 °) depends on the number of spatial periods, with fewer periods leading to higher horizontal bending angles. The vertical wave is a narrow-peak sinusoid with wide troughs with amplitudes ranging from 20 ° to 45 °.
Quantification of the spatial and temporal characteristics of the waves showed that kites use horizontal waves with 1-1.5 spatial periods and a waviness frequency of 1-1.7 Hz and vertical waves with 2-3 spatial periods and a waviness frequency of 2-3.4 Hz.
There is an additional component in air waviness, which scientists have called "dorsoventral bend," representing the up and down movement of the back of the body relative to the head. The angle of inclination of this bend was from -20 ° to 30 °. The dorsoventral bend was always present in the observed flights, but had no significant relationship with the number of spatial periods.
To accurately determine the degree of influence of the relationship between horizontal and vertical waves, as well as the influence of dorsoventral bending on the dynamics of flight, scientists created an anatomically accurate model of a snake in flight. Control over the model allows, according to scientists, to systematically check how the components of the undulation (the amplitude of the horizontal wave, the number of spatial periods and the frequency of undulation) affect the short-term and long-term dynamics of planning.
The horizontal wave is modeled as a sine wave with a flat top of large amplitude, and the vertical wave is modeled as a sinusoid of small amplitude:
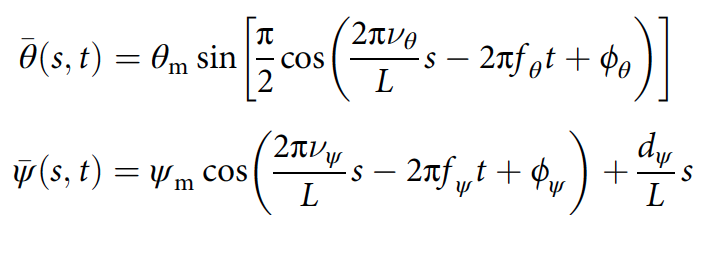
where θ m and ψ m are the maximum horizontal and vertical bending angles; ν is the number of spatial periods; f is the frequency of undulation; ϕ - phase shift; d ψ - dorsoventral bending angle; L - body length ( 2f , 2g ).
Horizontal and vertical waves are related in kinematic data ( 2 ): ν ψ = 2ν θ , f ψ = 2f θ and ϕ ψ = 2 (ϕ θ- π / 2). This greatly simplifies the model to 5 variables that determine the shape of the body: θ m , ψ m , ν θ , f θ and d ψ .
The position r = [x, y, z] of the body relative to the center of mass is calculated as follows: ∂ s x = cosψ̅sinθ̅, ∂ s y = -cosψ̅cosθ̅ and ∂ s z = sinψ̅.
The position of the center of mass R 0 and the orientation of the body ( yaw angles * , pitch and roll) are determined by integrating the equations of translational and rotational motion.
Yaw * - angular movements about the vertical axis.

where f L and f D - infinitesimal lifting and resistance forces; M A - aerodynamic moment; m is the mass of the snake.
To confirm that the mathematical model produces physically realistic results, the scientists simulated flights using parameters obtained from actual gliding observations of real kites (a comparison of simulations and observations is shown in the image below).

Image No. 3
Judging by comparison, the model works, but it has some minor inaccuracies that need to be addressed in the future.
To test the influence of undulation on the planning characteristics, two simulations were carried out: with f θ = 0 Hz (without undulation) and f θ= 1.2 Hz (average waviness frequency in snakes). In both cases, ν θ and θ m were varied ( 4a ).

Image №4 The
kinematic data of the snake body shape in the model made it possible to obtain 121 shapes with 1 ≤ ν θ ≤ 1.5 body waves and horizontal wave amplitudes in the range 90 ° ≤ θ m ≤ 119 °. Further, the observed body shapes were extracted from this array (middle part of the graph, separated along the diagonal; 4b ). The part of the graph that is highlighted below contains the "open" (resembling the letter S) body shapes, and the upper one - "closed" (resembling an infinity sign).
The vertical wave amplitude and dorsoventral angle were maintained at a constant level: 20 ° and 10 °, respectively. The simulation was considered complete when the center of mass of the body of the snake touched the ground (landing) or when any of the orientation angles exceeded the threshold value of 85 °. If this happened, then planning was considered unstable, i.e. not the same as in nature. During the simulation, both short-term dynamics (start height 10 m) and long-term dynamics (start height 75 m) with / without undulation were tested.
The model shows that air undulation has a positive effect on planning characteristics, usually increasing the horizontal and vertical distances traveled before the simulated snake becomes unstable.
Simulation of a flying snake gliding with and without undulation.
Short glides with a launch height of 10 m showed a good stability coefficient in the presence of waviness (94%). If the undulation was not included in the model, then only 50% of the flights were stable. Waviness also increases the gliding distance (from 4 m to 4.3 m).
When modeling planning from a height of 75 m, the undulation increased both horizontal and vertical distance before instability manifested in 86% of launches. In this case, waviness also increased flight distance in 92% of launches. Waviness also increased the average horizontal distance by 6.9 m.
To clarify the influence of the amplitude of the vertical wave and dorsoventral bending on the sliding dynamics, different values of these parameters were used in modeling and the results were considered.
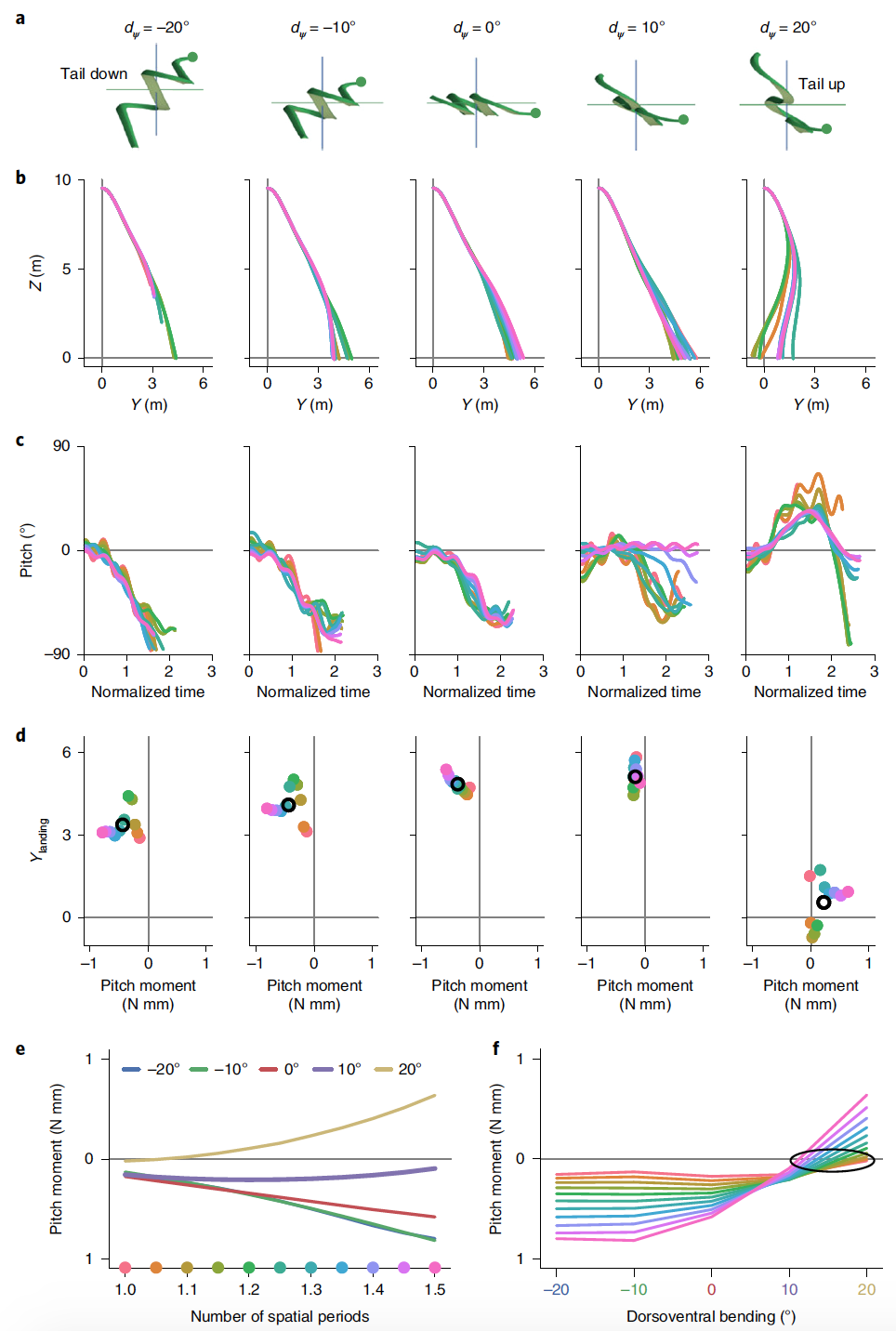
Image # 5
Planning was simulated with ψ m = 0 °, 10 ° and 20 ° and dorsoventral bend from -20 ° to 20 ° in 10 ° steps ( 5a ) for 11 different body shapes.
Vertical oscillation has relatively little effect on the gliding trajectory, while the dorsoventral bend has a significant impact.
Perfectly flat snake (ψ m= 0 °), which was never observed during experimental tests, showed the expected worst results. Increasing the amplitude of the vertical wave increased the planning efficiency due to the twisting of the cross-section in the plane, providing a more favorable angle for creating the force ( 2j ).
In contrast to the amplitude of the vertical wave, the dorsoventral bend had a noticeable effect on the planning characteristics, especially on the pitch.
At ψ m = −20 ° with the back of the body below the head, planning was not shallow; instead, it became unstable in height before falling by 10 m. At ψ m= 20 ° with the back of the body above the head, the trajectory is curved back, while some body shapes land behind the jump. Such poor planning is justified by an upward tilt of the body. Nevertheless, gliders with the above parameters had good rotational stability.
To verify the connection between the dorsoventral body bend, pitching and planning characteristics, a simulation was performed without rotation. Instead of solving a coupled nonlinear system of equations No. 4 and No. 5, scientists sampled the aerodynamic forces at different phases of the body during the wavy cycle. Further, equation No. 4 was integrated here, and the position and velocity of the center of mass were calculated.
In essence, this manipulation is a "virtual wind tunnel" experiment in which a dynamic model is used to calculate the distributed forces acting on a body as it accelerates. This method removes the relationship between translational and rotational motion in order to quantify the individual aerodynamic and inertial contributions to rotational motion.
With an increase in the dorsoventral bend from -20 ° to 10 °, the landing position of the simulated snake increases as the average pitch increases in the zero direction ( 5d ). At a 20 ° dorsoventral bend, the phase-averaged pitching moment becomes positive and gliding performance decreases.
For each dorsoventral bend angle, the planning efficiency and the mean oblique moment also depend on the shape used, in particular on the number of spatial periods and the amplitude of the horizontal wave. For any body shape at the moment of planning, the dorsoventral bend has a large effect on the average pitching moment, and with an increase in the number of spatial periods, the moments diverge, becoming more positive or negative depending on d ψ .
The marks of the phase-averaged pitch moments at 5e correspond to the upward slope or the slope shown at 5c and the resulting planning characteristics at 5b . At 5fIt is shown that for body shapes with the smallest spatial period, the average pitch moment will be the smallest.
From the above data, it can be assumed that the vertical wave causes the body to curl out of the plane, changing the local orientation of the “flattened wing” (the shape of the snake’s body during planning) using an air stream. Dorsoventral flexure controls the magnitude and sign of the aerodynamic principal moment that acts on the body. A flying kite can control the moment of pitch by changing the angle of bending of the dorsoventral region or the shape of a horizontal wave during flight.
Consequently, the dorsoventral curvature of the body plays an extremely important role in gliding stability, a successful landing and the ability to change the gliding trajectory right during its execution.

Image No. 6
Phase analysis by averaging allows one to quantify the relative contribution of aerodynamic and inertial moments to gliding dynamics.
Equations # 5 imply that the orientation of the body is influenced by both aerodynamic forces and changing mass distribution. The aerodynamic contribution ( 6a ) increases with time as the speed increases, while the inertial contribution ( 6b ) remains constant. Both moments are periodic, and only the pitch moment shows a nonzero phase average.
Initially, inertial moments predominate near the pitch and roll axes, but during one wave-like cycle their contribution decreases rapidly. The inertial moments of yaw, as a rule, are an order of magnitude greater than the aerodynamic moments of yaw and more than the inertial moments around other axes. Inertial moments of yaw arise due to a horizontal wave of large amplitude and a wide S-shaped body. This result suggests that flying kites can use inertial rotation as a maneuvering mechanism.
For a more detailed acquaintance with the nuances of the study, I recommend that you look into the report of scientists and additional materials to it.
And those who wish to familiarize themselves with the software used to analyze the planning of a flying kite can follow this link .
Epilogue
In this study, the researchers used the latest motion capture and 3D modeling techniques to create an anatomically accurate model of a flying snake.
Understanding the dynamics of a bird's flight was once also difficult, but it did not puzzle scientists as much as a flying kite does. In nature, there are not so many examples of wingless flights, and all of them are associated with the use of non-standard mechanisms that allow the animal to plan, and not fall like a stone to the ground.
In the case of flying kites, the waviness that occurs in the movement of crawling and swimming kites plays a very important role. An additional mechanism for stabilizing planning is the correction of the dorsoventral angle of the body bend. By combining these elements together, flying kites are able to fly from tree to tree, knowing exactly the place of future planting.
The authors of this work believe that their data not only allowed us to better understand the habits of decorated tree snakes, but also to gain additional inspiration for creating snake-like robots. Yes, there are already such robots. They crawl, can move over difficult surfaces and penetrate hard-to-reach places, but can they fly?
With such reasoning, our world will soon resemble the city of machines from the "Matrix", where extremely unusual (and slightly frightening) robotic creatures crawled along the walls, the purpose of which was difficult to understand. The desire of a person to make a robotic version of everything that surrounds him cannot be cheated. This is our nature - to understand everything, to know everything, to be able to create what nature did beautifully before us. If there is much more benefit than harm from robotic snakes, spiders, dogs and other robotic animals, such research is fully justified.
Thanks for watching, stay curious and have a great weekend everyone, guys!
Friday off-top:
, .
, .
Off-top 2.0:
, :)
, :)
A bit of advertising
Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending to your friends cloud-based VPS for developers from $ 4.99 , a unique analog of entry-level servers that was invented by us for you: The whole truth about VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps from $ 19 or how to divide the server? (options available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).
Dell R730xd 2 times cheaper at the Equinix Tier IV data center in Amsterdam? Only we have 2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV from $ 199 in the Netherlands!Dell R420 - 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB - from $ 99! Read about How to build the infrastructure of bldg. class using Dell R730xd E5-2650 v4 servers costing 9,000 euros per penny?