
Other cycle articles
AES — . I
ES — . II
AES — . III
AES — . IV
AES — . V.
ES — . II
AES — . III
AES — . IV
AES — . V.
The motive for publishing such detailed texts about the AES standard is to provide an opportunity to familiarize yourself with it in details, sufficient not only to develop an independent software implementation of the encryption algorithm, but also to create algorithms for possible cryptanalytic attacks on the cipher, i.e. for decrypting ciphergrams without knowing the key ...
Those publications that are available in the network, do not meet these goals, and cannot be used by me in the process of training specialists.
One of the main old (or even old) requirements for ciphers is to create an open (accessible for study) encryption algorithm and wrapping around it (modes, protocols, etc.) everything except the cipher key. The key is that which must be kept in the strictest confidence from everyone. In this case, the key does not have to be classified as "Secret". The limit of such a condition is that only the recipient of the ciphergram owns the key, he himself, in principle, must set it.
This condition is impracticable for symmetric encryption systems. And this is the fundamental difference between asymmetric (two-key) systems and symmetric ones, in which the source of information leakage about a key may not be the only one. It was noted earlier that AES is a simplified version of the RIJNDAEL cipher, and here we will use the full version in places.
AES (Key Schedule).
Choosing a key when encrypting a message is a responsible task. The general approach is that a random binary vector in a multidimensional vector space is chosen and used for the key. Often a number of encryption algorithms and ciphers are characterized by the presence of weak or invalid keys, which are revealed either during the development of ciphers or during their operation during additional research. algorithms by authors or cryptographers analysts and, accordingly, publications about it.
In turn, this imposes restrictions on the key generation procedure, which is undesirable, since it complicates it. The mathematical foundations for encryption are very similar to the mathematical foundations for generating keys, and you can read about them in detail here .
The chosen binary vector is called the cipher key and is converted to a “square” of 4x4 = 16 bytes. Then round keys are formed from it using two special procedures, which are used in the encryption / decryption processes, which are described in detail here .
One procedure is called Key Expansion, and the other is called Round Key Selection. A selected random binary vector with a fixed length is expanded. It is also important to carefully consider the choice of a random number generator, to test and approbate it.
Key expansion
The meaning of expanding the original (selected) key is to split it into non blocks (32 bits each) and then generate from them many new blocks of the same length for each round.
So, let the cipher key be selected (128 bits) AES = 2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c, for Nk = 4, which is represented by blocks of 4 bytes and its initial round extension has the form w [0 ] = 2b7e1516; w [1] = 28aed2a6; w [2] = abf71588; w [3] = 09cf4f3c. The w [i] symbol in the QC table, i = 0 (1) 43, indicates a column of 4 bytes of the round key.
An encryption session is the preparation and algorithmic transformation of a message, such as a letter. The text of the letter in bit representation is divided into blocks of fixed length Nb = 128, 192 or 256 bits. In AES, the block length is only 128 bits.
Then each block is represented by a square or (rectangle with 4 lines) and is encrypted separately for a fixed number of rounds Nr = Nr (Nb, Nk), which is a function of two variables: the length of the block Nb and the length of the key Nk, which can independently take values 128, 192, 256 bit.
The choice of the encryption key does not impose any restrictions on the bit sequence itself. Each of the Nr rounds uses its own pre-formed, or directly calculated, round key {w [i]}.
Round keys are formed from an encryption key using a special algorithm, which includes the Key Expansion procedure and the Round Key Selection procedure. Specifying round keys directly, bypassing these procedures, is unacceptable.
The essence and purpose of the first procedure is to convert a given original encryption key into a longer, expanded key (Expanded Key). The total number of bits of the extended key from which the round keys are selected is determined by the product K = Nk (Nr + 1) - the number of bits in the key block is multiplied by the number of rounds, increased by one.
Example 1 . Let Nb = Nk = 4, given blocks of length 4 × 32 = 128 bits, then Nr = 10.
Length K in bits for the extended key K = 128 ∙ 11 = 1408 bits.
The second procedure (RoundKey Selection) is a sequential selection of 32Nk, that is, 4 32-bit words from the extended key, i.e. the first round key is represented by the initial newly formed Nk words, the second round key by the following Nk words and so on until the last round.
Example 2... With the same initial data (see the previous example), the total length of the extended key in bytes contains Nk (Nr + 1) = 4 ∙ 11 = 44 four-byte words W (i),
i = 0 (1) Nk (Nr + 1) - 1 The rows of the QC table are numbered with natural numbers. The first row has number 4, since 4 rows (with numbers 0,1,2,3) with a cipher key are not included in the QC table.
Table Cipher key AES for all 10 rounds (see table QC below).

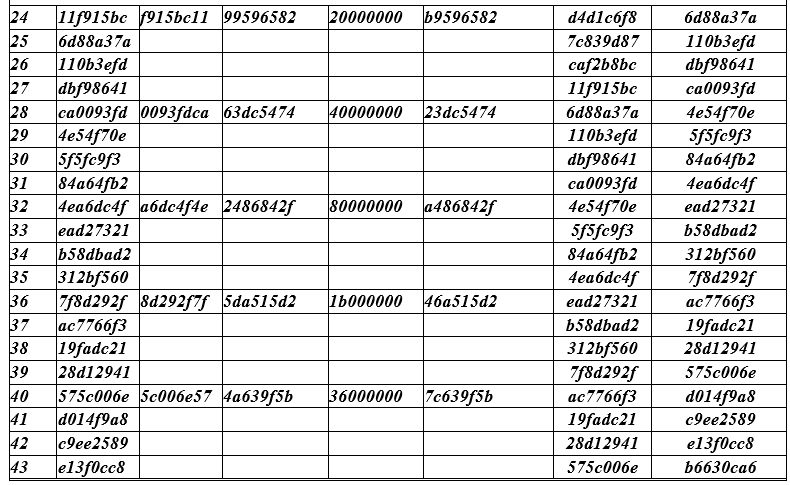
Rows of the table are divided into groups (4 rows each). In each group, all fields are filled in only one top line. In the next three lines, only the extreme (left and right) fields are filled. The values taken from the right margin of the line above it are entered into the left margin ( temp ) of the next and two subsequent lines.
Let's give an example of filling in the first row with the number i = 4 of the QC table. Left column - the current line numbers begin with the value (4) since the first 0,1,2,3 values are not included in the table. In general, the index (line number) i runs over the values i = 0 (1) Nk (Nr + 1) -1 or i = 0 (1) 43 in total 44 words of 32 bits.
To the temp columnthe value w [i-1] = 09cf4f3c is placed and by rotation (cyclic shift of one byte) RotWord () we get the value CF4F3C09, which is placed in the 3rd column. The 4th column contains the result of 8A84EB01 replacing bytes of SubBytes of the values from the 3rd column , i.e., CF → 8A; 4F → 84; 3C → EB; 09 → 01 => 8A84EB01.
Each 4th row of the table in the 5th column is filled with the value Rcon [i / Nk], a constant calculated by the formula Rcon (J) = 01000000, j = [i / Nk] = 2 j-1 = 2 0 = 1) the value 01 00 00 00 is written out of 4 byte words, the first byte of which is 2 0 = 1, i.e. 0000 0001 2 , the remaining bytes of this 32-bit word are zero.
Column 6 field contains the sum (XOR) of the 4th and 5th fields 8A84EB01 + 01000000 = 8B84EB01;
Column 7 field contains W [i - Nk] = W [4 - 4] = W [0] = 2B7E1516;
Column 8 field contains the sum of the fields of columns 6 and 7 W [i = 4] = 884EB01 + 2B7E1516 = A0FAFE17;
And now we will consider the named procedures in detail and in detail.
Key Expansion Procedure
Let's consider in detail the procedure for generating an Expanded Key from the original cipher key. The formally extended key W will be described by the sequence of blocks W [i], i = 0 (1) Nk (Nr + 1) -1, 4-byte words (round keys) contained in the last column of the QC table, in which the first Nk are 32-bit words represent the original key, that is,
W = {W [0], W [1], W [2], W [3], W [4], ..., W [K-1]}
Subsequent i-th words are formed recursively from previous words in accordance with an expression in which the summation is XOR.
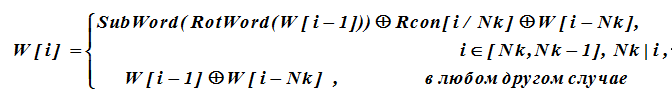 ...
...
For the words W [i] of the key, the index of which is a multiple of Nk, the values of W [i-1] are subjected to an additional transformation before performing the XOR operation. This transformation is described as follows.
The transformation description contains functions:
RotWord () - byte cyclic shift of the 32-bit word a (0) a (1) a (2) a (3) according to the rule
{a (0) a (1) a (2) a (3)} → {a (3) a (0) a (1) a (2)};
SubWord () - byte replacement a (j) with elements of the S-box of the SubBytes () function, for example, byte (af) is replaced with byte s (a, f) from the S-box; the action is the same as when processing a message,
Rcon [j] - the XOR term is equal to 2 j-1 .

Highlighted positions that are multiples of Nb, the values of which are formed using the SubWord (), RotWord (), Rcon () functions. Positions W [0] –W [3] are filled in according to the given initial data, all subsequent ones are calculated by the ratio for W [i].
Round Key Selection
Round key selection (RoundKeySelection). For the current round with number r. The round key is chosen as {W [Nb (r) -1], ..., W [Nb (r + 1) - 1]},
r = 1 (1) Nr.
Here we note that the general encryption algorithm provides for different variants of the sets of variables Nb, Nk, Nr. For a specific implementation of a fixed version, it can be significantly simplified. The round key can be computed on the fly, which does not require a lot of memory to store the entire sequence W. You can limit yourself to a buffer of Nk words.
Example 3 . Let us explain the above theoretical propositions by a numerical example. Let, as before, Nb = Nk = 4, Nr = 10. The cipher key is given as a hexadecimal sequence K = 2b7e1516 282ed2a6 abf71588 09cf4f3c

The architecture "square" and byte-oriented computations are defined by the following table.
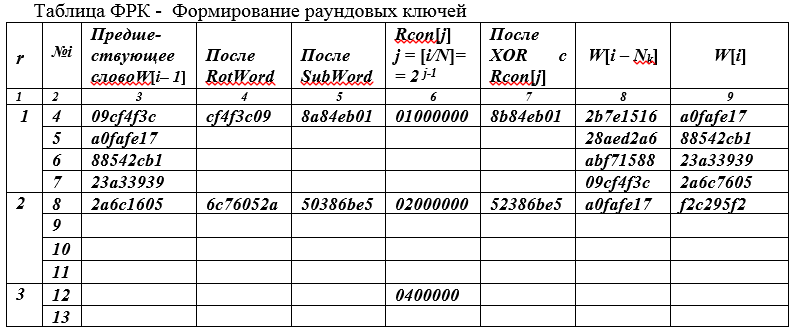
The left column has been added to the table - the number (r) of the round.
In the first line r = 1, i = 4, the preceding byte W [i-1] = W [3] is written in the third column, ie the last byte of the K cipher key. Since the index i = 4 is a multiple of Nk = 4, then in column 6 we write (Rcon (J) = 01000000, j = [i / Nk] = 2 j-1 = 2 0 = 1) the value 01 00 00 00 4- is written x byte word, the first byte of which is 2 0 = 1, i.e. 0000 0001, the remaining bytes of this 32-bit word are zero.
In the fourth column of the table, we enter the values from the previous column, but cyclically shifted by 1 byte to the left (word rotation - RotWord). The fifth column contains the result of a byte replacement of the values of the previous column by the values of bytes from the S - block (SubWord function - byte replacement). After that, mod2 (XOR) addition is done of the contents of columns 5 and 6, 8a84eb01 + 0100 0000 = 8b84eb01, and the summation result is entered in column 7.
In the binary representation of byte 0000 0001 2 = 01 16 the least significant bits are located on the right.
Column 8 contains the value of the word W [i-Nk] = W [0] (for the first line, this is the value of the first (left byte) 4-byte word of the encryption key W [0]), which is added by the XOR operation 8b 84 eb 01+ 2b 7e 15 16 = a0 fa fe 17 with the content of 7 columns. The result of the summation (column 9) is just the first of the four, 4-byte words of the round key of the first round.
The other three words of the round key of the first round are formed without using the function of cyclic shift, replacement and Rcon [j], since their numbers are not multiples of Nk. The content of column 9 is transferred to the third column of the next line of the table.
Definition of Rcon [j]. This procedure is performed according to a special algorithm, the actions of which we will illustrate with examples. The argument j of the function Rcon [j] is integer and is determined by the current value of the variable i, the key word number. Obviously
j = 1, 2, 3,… for i = Nk, 2Nk, 3Nk,….
Since Nk in our example is 4, we have integer values of j for i = 4, 8, 12. Further, for each integer j, Rcon [j] = 2 j-1 = 1, 2, 4, 8, 16, ....
Doubling of values is allowed as long as Rcon [j] is an element of the GF (2 8 ) field .
For i> 32 we get j> 8. Values outside the field must be returned to the field. This is achieved by reducing the polynomial representation of the elements of the field Rcon [j] (modφ (x)).
Example 4. Let i = 32, 36, 40. Then j = 8, 9, 10. These values are outside the field. We return them to the field by reduction modulo φ (x) and calculate the required values.
Let us determine the corresponding values of Rcon [j]. The results of the calculations are summarized in a table.

This completes the review of the steps for generating round AES cipher keys.