We continue to familiarize ourselves with various heaps and sorting algorithms using these heaps. Today we have the so-called tournament tree.
The main idea of ​​Tournament sort is to use a relatively small (compared to the main array) auxiliary heap, which acts as a priority queue. In this heap, the elements at the lower levels are compared, as a result of which the smaller elements (in this case, the MIN-HEAP tree) go up, and the current minimum of the portion of the array elements that fall into this heap pops up to the root. The minimum is transferred to an additional array of "winners", as a result of which the remaining elements are compared / moved in the heap - and now a new minimum is at the root of the tree. Note that with such a system, the next minimum is greater in value than the previous one - then a new ordered array of "winners" is easily assembled, where new minimums are simply added to the end of the additional array.
EDISON .
, . , .
computer science ;-)
Transferring the minima to the additional array leads to the fact that vacant places for the next elements of the main array appear in the heap - as a result, all elements are processed in the order of the queue.
The main subtlety is that in addition to the “winners” there are also “losers”. If some elements have already been transferred to the array of "winners", then if the unprocessed elements are smaller than these "winners", then there is no point in sifting them through the tournament tree at this stage - inserting these elements into the array of "winners" will be too expensive (in You cannot end them, but to put them at the beginning, you have to shift the previously inserted minimums). Such elements that did not manage to fit into the array of “winners” are sent to the array of “losers” - they will go through the tournament tree in one of the following iterations, when all actions are repeated for the remaining losers.
It’s not easy to find an implementation of this algorithm on the Internet, but on YouTube a clear and pretty implementation on Ruby was found. Java code is also mentioned in the "Links" section, but it doesn't look so readable there.
#
require_relative "pqueue"
#
MAX_SIZE = 16
def tournament_sort(array)
# , ""
return optimal_tourney_sort(array) if array.size <= MAX_SIZE
bracketize(array) # , ""
end
#
def bracketize(array)
size = array.size
pq = PriorityQueue.new
#
pq.add(array.shift) until pq.size == MAX_SIZE
winners = [] # ""
losers = [] # ""
#
until array.empty?
# "" ?
if winners.empty?
# ""
winners << pq.peek
#
pq.remove
end
# , ""
if array.first > winners.last
pq.add(array.shift) #
else # ""
losers << array.shift # ""
end
# , ""
winners << pk.peek unless pk.peek.nil?
pq.remove #
end
# , - ?
until pq.heap.empty?
winners << pq.peek # ""
pq.remove #
end
# "" , , ,
# "" -
return winners if losers.empty?
# , ""
# ""
array = losers + winners
array.pop while array.size > size
bracketize(array) #
end
#
def optimal_tourney_sort(array)
sorted_array = [] #
pq = PriorityQueue.new
array.each { |num| pq.add(num) } # -
until pq.heap.empty? # -
sorted_array << pq.heap[0]
pq.remove #
end
sorted_array #
end
#
if $PROGRAM_NAME == __FILE__
#
shuffled_array = Array.new(30) { rand(-100 ... 100) }
#
puts "Random Array: #{shuffled_array}"
#
puts "Sorted Array: #{tournament_sort(shuffled_array)}"
endThis is a naive implementation, in which after each division into "losers" and "winners" these arrays are combined and then all actions are repeated again for the combined array. If in the combined array there are “losing” elements first, then sifting through the tournament pile will order them together with the “winners”.
This implementation is quite simple and intuitive, but you cannot call it effective. Sorted "winners" go through the tournament tree more than once, which seems obviously unnecessary. I assume that the time complexity here is log-quadratic,
Multipath merge option
The algorithm is noticeably accelerated if the ordered elements passing through the sieve are not passed through tournament races repeatedly.
After the unordered array is split into sorted "winners" and unsorted "losers", the whole process is repeated only for the "losers". At each new iteration, a set of arrays with "winners" will be accumulated and this will continue until at some step there are no "losers" left. After that, all that remains is to merge all arrays of "winners". Since these arrays are all sorted, this merge proceeds with minimal effort.
In this form, the algorithm may already find a useful application. For example, if you have to work with big data, then in the course of the process, using the tournament heap, packets of ordered data will be released, with which you can already do something while everything else is being processed.
Each of the n elements of the array goes through the tournament tree only once, which takes
In the season finale
The series on heap sorts is almost complete. It remains to talk about the most effective of them.
References
Tournament sort
Priority queue
Tournament sort in Java
The Theory Behind the The Theory Behind the z/Architecture Sort Assist Instructions
Using Tournament Trees to Sort
Tournament Sort Demo Ruby
Tournament Sort Visualization
Tournament Sort Data Structure UGC NET DS
Tournament Sort Algorithm — a Heapsort variant
:
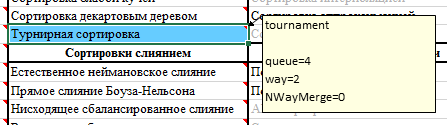
Today's sorting has been added to the AlgoLab application, who uses it - update the excel file with macros.
In the comments to the cell with the name of the sort, you can specify some settings.
The variable way is a multi- way tournament tree (just in case, it is possible to make this tree not only binary, but also ternary, quaternary, and pentary).
The variable queue is the size of the initial queue (the number of nodes at the lowest level of the tree). Since the trees are full, if, for example, with way = 2 you specify queue = 5, then the queue size will be increased to the nearest power of two (in this case, up to 8). NWayMerge
variable takes the value 1 or 0 - with the help of it it is indicated whether to use multi-path merging or not.